3. Решите неравенство 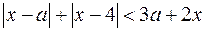 .
.
Решение. Перепишем неравенство в виде 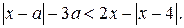 (1)
(1)
1. Рассмотрим функции 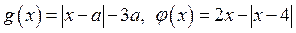 .
.
1) Графиком функции 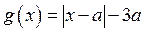 , является «подвижный уголок» с вершиной в точке
, является «подвижный уголок» с вершиной в точке 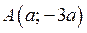 и со сторонами
и со сторонами
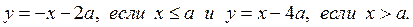
2) Имеем
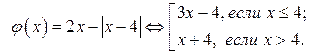
График функции 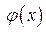 проходит через точку
проходит через точку 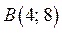 .
.
Отметим: прямые 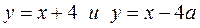 параллельны.
параллельны.
Исходное неравенство имеет решение тогда и только тогда, когда 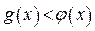 (график функции
(график функции 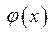 расположен выше графика функции
расположен выше графика функции 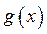 ).
).
2. График функции 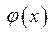 проходит через точку А
проходит через точку А 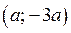 (вершина «подвижного уголка»), если
(вершина «подвижного уголка»), если
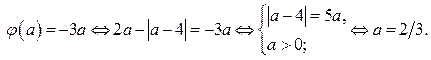
График функции 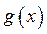 проходит через точку
проходит через точку 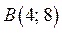 , если
, если
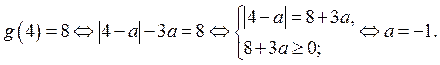
Ось абсцисс точками 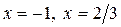 разбивается на 3 промежутка:
разбивается на 3 промежутка: 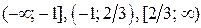 .
.
3. Рассмотрим следующие случаи.
1) Пусть 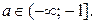
 Если
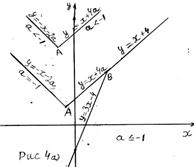
Если 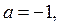 то при
то при 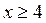 графики функций
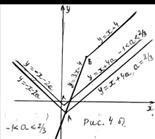
графики функций 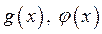 совпадают (рис. 4 а)), тогда неравенство (1) не имеет решений (так как
совпадают (рис. 4 а)), тогда неравенство (1) не имеет решений (так как 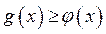 ) Если
) Если 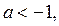 то
то 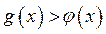 (рис. 4 а)), тогда неравенство (1) не имеет решений.
(рис. 4 а)), тогда неравенство (1) не имеет решений.
Итак, если 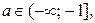 то неравенство (1) не имеет решений.
то неравенство (1) не имеет решений.
2) Пусть 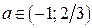 . Из рисунка 4б) следует: если
. Из рисунка 4б) следует: если 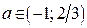 , то для любого
, то для любого 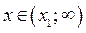 , где
, где 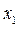 абсцисса точки пересечения прямых
абсцисса точки пересечения прямых 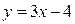 и
и 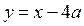 выполняется неравенство
выполняется неравенство 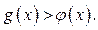 Тогда для
Тогда для 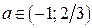 решениями неравенства (1) являются
решениями неравенства (1) являются 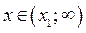 . Абсциссу
. Абсциссу 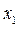 точки пересечения прямых
точки пересечения прямых 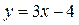 и
и 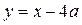 найдём из уравнения
найдём из уравнения 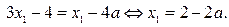
 Итак, если
Итак, если 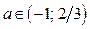 , то решениями неравенства (1) являются
, то решениями неравенства (1) являются 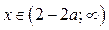 .
.
 3) Пусть
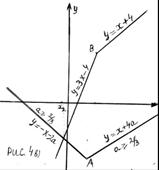
3) Пусть 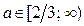 . Из рисунка 4в) следует: если
. Из рисунка 4в) следует: если 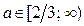 , то для любого
, то для любого 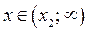 , где
, где 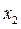 абсцисса точки пересечения прямых
абсцисса точки пересечения прямых 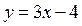 и
и 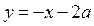 , выполняется неравенство
, выполняется неравенство 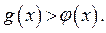 Тогда для
Тогда для 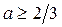 решениями неравенства (1) являются
решениями неравенства (1) являются 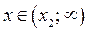 . Абсциссу
. Абсциссу 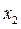 точки пересечения прямых
точки пересечения прямых 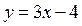 и
и 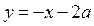 найдём из уравнения
найдём из уравнения 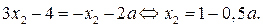
Итак, если 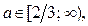 то решениями неравенства (1) являются
то решениями неравенства (1) являются 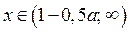 .
.
Ответ. Если 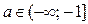 , то нет решений; если
, то нет решений; если 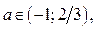 , то
, то 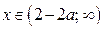 ; если
; если 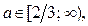 то
то 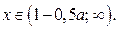
4. Решите неравенство 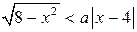 . (1)
. (1)
Решение. ОДЗ неравенства: 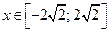 (находим из неравенства
(находим из неравенства 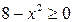 ).
).
Так как неравенство (1) не имеет решений, если 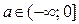 (в этом случае
(в этом случае 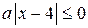 ), то рассмотрим это неравенство при
), то рассмотрим это неравенство при 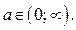
1. Рассмотрим функции 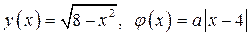 .Имеем
.Имеем
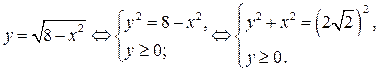
Графиком функции 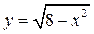 является полуокружность, расположенная выше оси абсцисс, с центром в точке (0; 0) и радиусом, равным
является полуокружность, расположенная выше оси абсцисс, с центром в точке (0; 0) и радиусом, равным 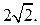
Графиком функции 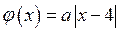 является «уголок с подвижными сторонами» с вершиной в точке
является «уголок с подвижными сторонами» с вершиной в точке 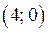 и со сторонами
и со сторонами
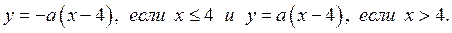
Исходное неравенство имеет решение тогда и только тогда, когда 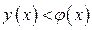 .
.
2. Рассмотрим следующие случаи.
1) Графики функций 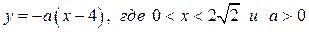 ,
, 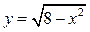 пересекаются не более чем в одной точке, если имеет не более одного решения система
пересекаются не более чем в одной точке, если имеет не более одного решения система
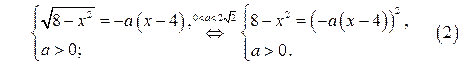
Система (2) имеет не более одного решения, если имеет не более одного решения квадратное уравнение
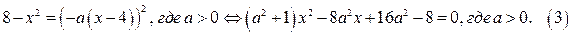
Квадратное уравнение (3) имеет не более одного решения, если при 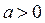 дискриминант этого уравнения
дискриминант этого уравнения 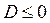 . Имеем
. Имеем
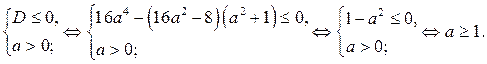
Если 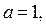 то решением квадратного уравнения (3) является
то решением квадратного уравнения (3) является 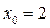 ; если
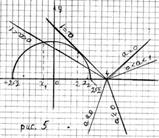
; если 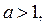 то уравнение (3) не имеет решений. Из рисунка 5 следует: решениями неравенства (1), если
то уравнение (3) не имеет решений. Из рисунка 5 следует: решениями неравенства (1), если 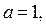 являются
являются 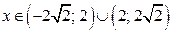 ; если
; если 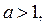 то
то 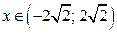 , так как в этом случае
, так как в этом случае 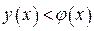 .
.
2) Графики функций 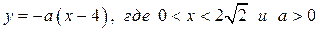 ,
, 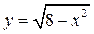 пересекаются в двух точках, если квадратное уравнение (3) имеет два решения. Квадратное уравнение (3) имеет два решения, если
пересекаются в двух точках, если квадратное уравнение (3) имеет два решения. Квадратное уравнение (3) имеет два решения, если
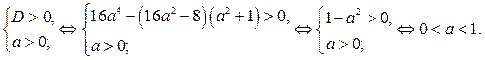
 Итак, если
Итак, если 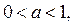 то решениями квадратного уравнения (3) являются
то решениями квадратного уравнения (3) являются
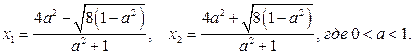
Из рисунка 5 следует: решениями неравенства (1), если 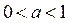 , являются
, являются 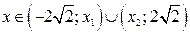 .
.
Ответ. Если 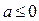 , то нет решений; если
, то нет решений; если 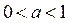 , то
, то 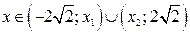 ; если
; если 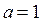 , то
, то 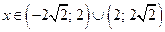 ; если
; если 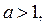 то
то 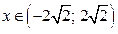
 2015-03-22
2015-03-22 349
349








