1. Решите неравенство 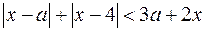 . (1)
. (1)
Решение. Рассмотрим следующие три случая.
1. Если 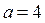 , то неравенство (1) принимает вид
, то неравенство (1) принимает вид
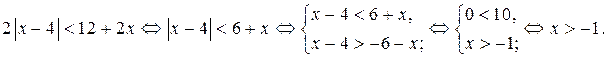
Если 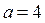 , то решениями неравенства (1) являются
, то решениями неравенства (1) являются 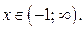
2. Если 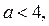 то неравенство (1) равносильно системе
то неравенство (1) равносильно системе
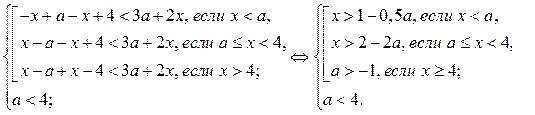
1) Рассмотрим неравенство 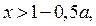 где
где 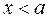 и
и 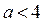 . (2)
. (2)
а) Если 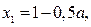 где
где 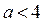 , принадлежит интервалу
, принадлежит интервалу 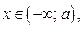 где
где 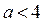 , то решением неравенства (2), а значит и неравенства (1), будет интервал
, то решением неравенства (2), а значит и неравенства (1), будет интервал 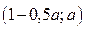 , если
, если
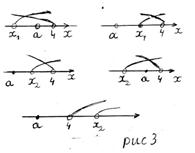
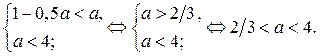
Решениями неравенства (1) являются 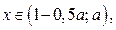 где
где 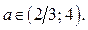
б) Если 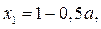 где
где 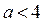 , не принадлежит интервалу
, не принадлежит интервалу 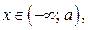 где
где 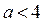 , то неравенство (2) на интервале
, то неравенство (2) на интервале 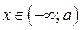 не имеет решений.
не имеет решений.
2) Рассмотрим неравенство 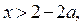 где
где 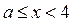 и
и 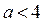 . (3)
. (3)
а) Если 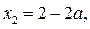 где
где 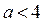 , принадлежит промежутку
, принадлежит промежутку 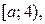 где
где 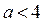 , то решением неравенства (3), а значит и неравенства (1), будет промежуток
, то решением неравенства (3), а значит и неравенства (1), будет промежуток 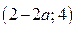 , если
, если
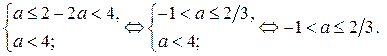
Решениями неравенства (1) являются 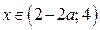 , если
, если 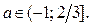
б) Если 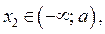 где
где 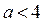 , то решением неравенства (3), а значит и неравенства (1), будет промежуток
, то решением неравенства (3), а значит и неравенства (1), будет промежуток 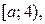 если
если
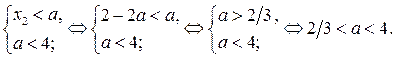
Решениями неравенства (1) являются 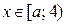 , если
, если 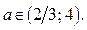
в) Если 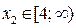 , где
, где 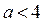 , то неравенство (3) на промежутке
, то неравенство (3) на промежутке 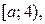 не имеет решений.
не имеет решений.
3) Рассмотрим неравенство 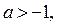 где
где 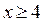 и
и 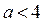 .
.
В этом случае решениями неравенства 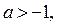 если
если 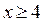 , а значит и неравенства (1), являются
, а значит и неравенства (1), являются 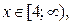 если
если 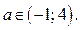
Из 1) – 3) следует: если 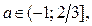 то
то 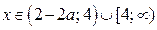 =
= 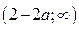 ;
;
если 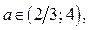 то
то 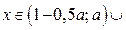
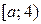
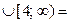
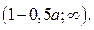
3. Если 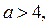 то неравенство (1) равносильно системе
то неравенство (1) равносильно системе
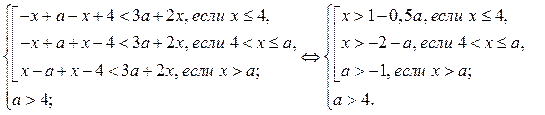
1) Рассмотрим неравенство 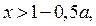 где
где 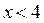 и
и 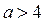 (4).
(4).
а) Если 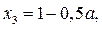 где
где 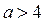 , принадлежит промежутку
, принадлежит промежутку 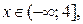 , то решением неравенства (4), а значит и неравенства (1), будет промежуток
, то решением неравенства (4), а значит и неравенства (1), будет промежуток 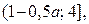 если
если
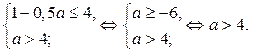
Решениями неравенства (1) являются 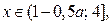 где
где 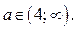
б) Если 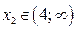 , где
, где 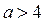 , то неравенство (4), не имеет решений.
, то неравенство (4), не имеет решений.
2) Рассмотрим неравенство 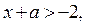 где
где 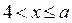 ,
, 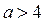 . Решениями последнего неравенства, а значит и неравенства (1), являются
. Решениями последнего неравенства, а значит и неравенства (1), являются 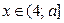 . (отметим: если
. (отметим: если 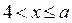 и
и 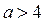 , то
, то 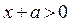 )
)
3) Рассмотрим неравенство 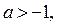 где
где 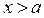 ,
, 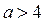 . Решениями последнего неравенства, а значит и неравенства (1), являются
. Решениями последнего неравенства, а значит и неравенства (1), являются 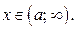
Из 1) – 3) следует:
если 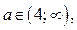 то
то 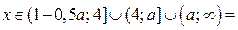
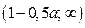 .
.
Из 1. и 3. следует: решениями неравенства (1) являются 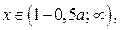 если
если 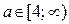 (так как, если
(так как, если 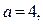 то
то 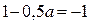 ).
).
Ответ. Если 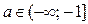 , то нет решений; если
, то нет решений; если 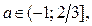 , то
, то 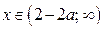 ; если
; если 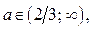 то
то 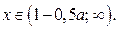
2. Решите неравенство 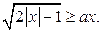 (1)
(1)
Решение. ОДЗ неравенства 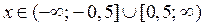 (следует из неравенства
(следует из неравенства 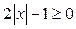 ).
).
1. Если 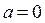 , то неравенство (1) принимает вид
, то неравенство (1) принимает вид 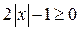 .Решениями последнего неравенства являются
.Решениями последнего неравенства являются 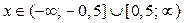 .
.
Замечание. Точки 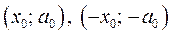 одновременно являются решениями неравенства (1) (так как
одновременно являются решениями неравенства (1) (так как 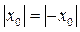 и
и 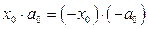 ). Это означает, если
). Это означает, если 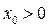 является решением неравенства (1) при
является решением неравенства (1) при 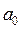 , то
, то 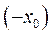 является решением этого неравенства при
является решением этого неравенства при 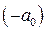 .
.
2. Пусть 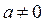 .
.
Рассмотрим неравенство (1) при 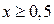 .
.
Если 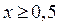 , то неравенство (1) принимает вид
, то неравенство (1) принимает вид 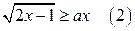 .
.
Неравенство (2) равносильно совокупности
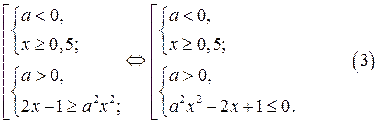
а) Решениями первой системы совокупности (3), а значит и неравенства (2), являются 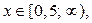 если
если 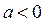 . Тогда из замечания следует, что решениями неравенства (1) также являются
. Тогда из замечания следует, что решениями неравенства (1) также являются 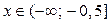 , если
, если 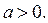
б) Рассмотрим вторую систему совокупности (3).
Корнями квадратного уравнения 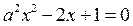 , где
, где 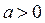 , являются
, являются 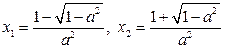 , где
, где 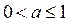 .
.
Докажем, что 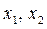 принадлежат промежутку
принадлежат промежутку 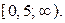 Отметим: так как
Отметим: так как 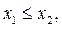 то, если
то, если 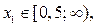 то и
то и 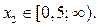 Имеем
Имеем
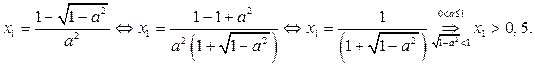
Получили, что 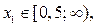 а тогда и
а тогда и 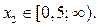
Решениями второй системы совокупности (3), а значит и неравенства (2), являются 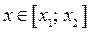 , если
, если 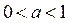 , и.
, и. 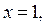 если
если 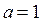 . Тогда из замечания следует, что решениями неравенства (1), также являются
. Тогда из замечания следует, что решениями неравенства (1), также являются 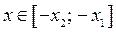 , если
, если 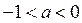 , и
, и 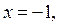 если
если 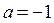 .
.
Ответ. Если 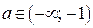 , то
, то 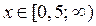 ; если
; если 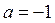 , то
, то 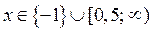 ; если
; если 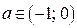 , то
, то 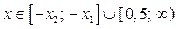 ; если
; если 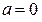 , то
, то 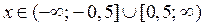 ; если
; если 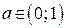 , то
, то 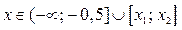 ; если
; если 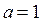 , то
, то 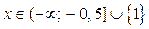 ; если
; если 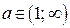 , то.
, то. 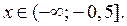
 2015-03-22
2015-03-22 351
351








