Определение. Функция 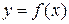 , определённая на множестве Х, принимает на этом множестве наименьшее значение в точке
, определённая на множестве Х, принимает на этом множестве наименьшее значение в точке 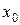 , если точка
, если точка 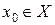 и
и 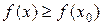 для любого
для любого 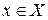 .
.
Определение. Функция 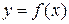 , определённая на множестве Х, принимает на этом множестве наибольшее значение в точке
, определённая на множестве Х, принимает на этом множестве наибольшее значение в точке 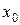 , если точка
, если точка 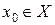 и
и 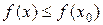 для любого
для любого 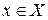 .
.
При решении неравенств методом оценки часто пользуются следующим.
1. Пусть m наименьшее значение функции 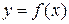 на множестве Х.
на множестве Х.
Неравенство 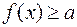 (
(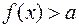 ) выполняется для всех
) выполняется для всех 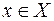 ,если а не больше (меньше) наименьшего значения функции
,если а не больше (меньше) наименьшего значения функции 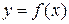 на множестве Х, то есть, если
на множестве Х, то есть, если 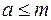
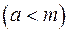 .
.
Неравенство 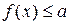 (
(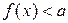 ) имеет решение,если
) имеет решение,если 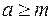
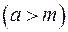 .
.
2. Пусть M наибольшее значение функции 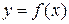 на множестве Х.
на множестве Х.
Неравенство 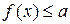 (
(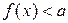 ) выполняется для всех
) выполняется для всех 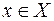 ,если а не меньше (больше) наибольшего значения функции
,если а не меньше (больше) наибольшего значения функции 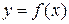 на множестве Х, то есть, если
на множестве Х, то есть, если 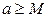
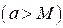 .
.
Неравенство 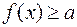 (
(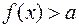 ) имеет решение,если
) имеет решение,если 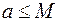
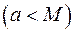 .
.
Замечание. Неравенство между средним арифметическим и средним геометрическим (неравенство Коши):
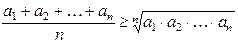 , где
, где  .
.
Среднее арифметическое положительных чисел не меньше их среднего геометрического. Равенство имеет место тогда и только тогда, когда 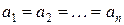 .
.
7. Найдите все значения параметра а, при которых для всех 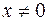 выполняется неравенство
выполняется неравенство 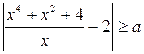
Решение. 1. Пусть 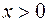 .Найдём наименьшее значение функции
.Найдём наименьшее значение функции 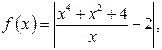 где
где 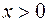 .
.
1) Рассмотрим функцию
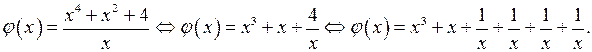
Воспользуемся неравенством Коши. Так как 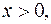 то
то
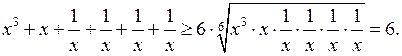
Итак, 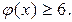 Равенство достигается тогда и только тогда, когда
Равенство достигается тогда и только тогда, когда 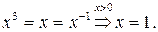
2) Оценим функцию 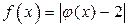 на интервале
на интервале 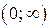 . Для этого воспользуемся неравенством
. Для этого воспользуемся неравенством 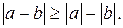
Так как 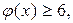 если
если 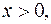 то
то 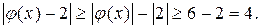
Итак, для любого 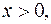 выполняется неравенство
выполняется неравенство 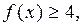 причём, если
причём, если 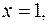 то
то 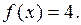 Это означает, что число 4 является наименьшим значением функция
Это означает, что число 4 является наименьшим значением функция 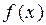 на интервале
на интервале 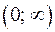 .Тогда для любого числа а, удовлетворяющему неравенству
.Тогда для любого числа а, удовлетворяющему неравенству 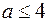 ,на интервале
,на интервале 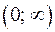 выполняется неравенство
выполняется неравенство 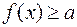
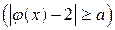 .
.
2. Пусть 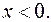 Очевидно, что
Очевидно, что 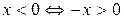 , а так же очевидно, что
, а так же очевидно, что 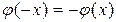 .
.
Оценим функцию 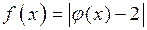 на интервале
на интервале 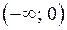 .
.
Имеем
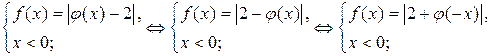
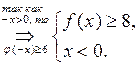
Итак, для любого 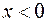 выполняется неравенство
выполняется неравенство 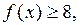 причём, если
причём, если 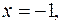 то
то 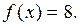 Это означает, что число 8 является наименьшим значением функция
Это означает, что число 8 является наименьшим значением функция 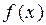 на интервале
на интервале 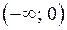 .Тогда для любого числа а, удовлетворяющему неравенству
.Тогда для любого числа а, удовлетворяющему неравенству 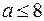 ,на интервале
,на интервале 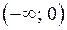 выполняется неравенство
выполняется неравенство 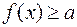 , то есть выполняется неравенство
, то есть выполняется неравенство 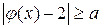 .
.
Итак: неравенство 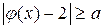 выполняется для любого
выполняется для любого 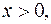 если
если 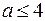 и это неравенство выполняется для любого
и это неравенство выполняется для любого 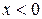 , если
, если 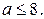 Тогда исходное неравенство выполняется для любого
Тогда исходное неравенство выполняется для любого 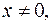 если
если 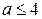 .
.
Ответ. 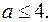
Оценим функцию 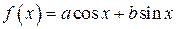 , где
, где 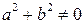 .
.
Воспользуемся методом введения дополнительного угла. Имеем
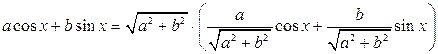 .
.
Так как 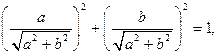
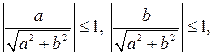 то можно положить
то можно положить 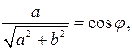
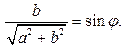
Тогда 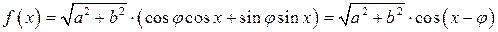 .
.
Так как 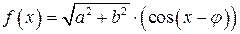 и
и 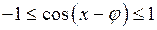 , то
, то
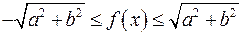 .
.
Итак, наименьшее значение функции 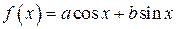 , где
, где 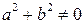 , равно
, равно 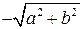 , а наибольшее значение равно
, а наибольшее значение равно 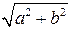 .
.
Наименьшее значение функции 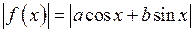 , где
, где 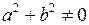 , равно нулю, а наибольшее значение, равно
, равно нулю, а наибольшее значение, равно 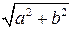 .
.
8. Найдите все значения параметра b, при которых неравенство 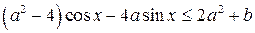 имеет решение для любого а.
имеет решение для любого а.
Решение. Наименьшее значение функции 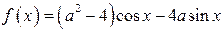 , равно
, равно
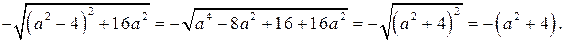
Итак, наименьшее значение функции 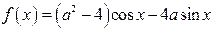 , равно
, равно 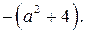 Тогда исходное неравенство
Тогда исходное неравенство 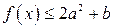 имеет решение, если
имеет решение, если 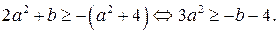
Неравенство 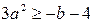 выполняется при любом а, если
выполняется при любом а, если 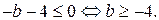
Ответ. 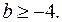
9. Найдите все значения параметра а, при которых для любых значений 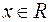 выполняетсянеравенство
выполняетсянеравенство 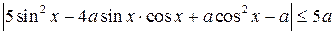
Решение. Преобразуем 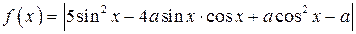 .
.
Для этого воспользуемся следующими формулами
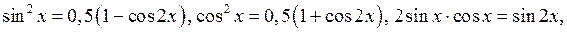
Таким образом, имеем
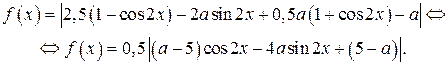
Найдём наибольшее значение функции 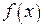 , для этого воспользуемся неравенствами:
, для этого воспользуемся неравенствами: 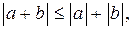
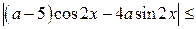
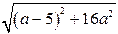 .
.
Имеем
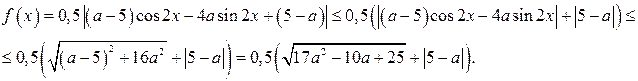 Так как
Так как 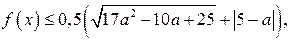 то наибольшее значение функции
то наибольшее значение функции 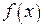 равно
равно 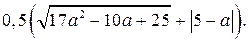 Тогда решением неравенства
Тогда решением неравенства 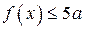 является любое
является любое 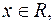 если
если
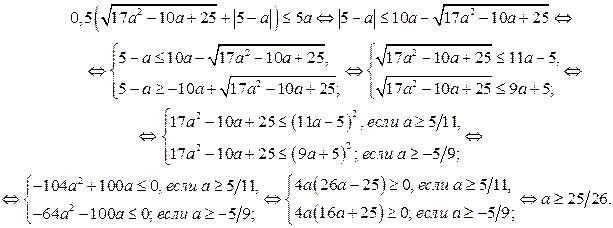 Итак, искомые значения
Итак, искомые значения 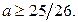
Ответ. 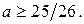
Замечание. Если в задаче требуется определить значения параметра, при которых неравенство (уравнение, система) выполняется при всех значениях переменной из множества Х, то подставив какое-нибудь конкретное значение из Х, получим значения параметра, среди которых находятся искомые значения.
Если получаем конечное число значений параметра, то каждое из них требует проверки.
Если получаем бесконечное число значений параметра, то для нахождения искомых значений параметра надо провести дополнительные исследования.
10. Найдите все значения параметра а, при которых неравенство 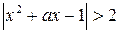 не имеет решений на отрезке
не имеет решений на отрезке 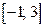 .
.
Решение. Рассмотрим задачу, равносильную исходной.
Найдите все значения параметра а, при которых неравенство 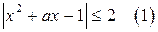 выполняется при всех
выполняется при всех 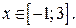
Рассмотрим неравенство (1) при 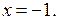 Имеем
Имеем
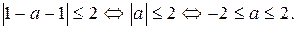
Искомые значения параметра а могут принадлежать отрезку 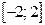 .
.
2. Рассмотрим неравенство (1) при 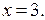 Имеем
Имеем
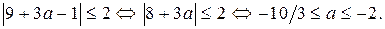
Искомые значения параметра а могут принадлежать отрезку 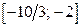 .
.
Из 1. и 2. следует: неравенство (1) выполняется при всех 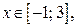 если
если 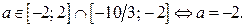
Проверим, будет ли выполняться неравенство (1) при всех 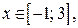 если
если 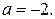 Имеем
Имеем
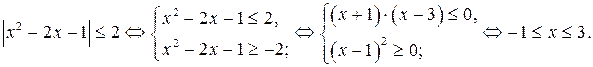
Ответ. 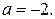
11. Найдите все значения параметра а, при которых в множестве решений неравенства 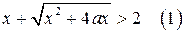 содержится отрезок
содержится отрезок 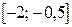 .
.
Решение. 1. Рассмотрим неравенство (1) при 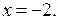 Имеем
Имеем
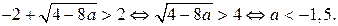
Искомые значения параметра а могут принадлежать интервалу 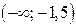 .
.
2. Рассмотрим неравенство (1) при 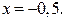 Имеем
Имеем
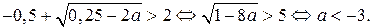
Искомые значения параметра а могут принадлежать интервалу 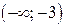 .
.
Так как 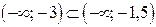 , то предположим, что искомые значения параметра а принадлежат интервалу
, то предположим, что искомые значения параметра а принадлежат интервалу 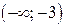 .
.
3. Оценим левую часть неравенства (1), если 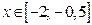 и
и 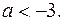
Рассмотрим функцию 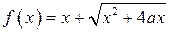 , где
, где 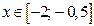 и
и 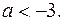
Найдём промежутки монотонности функции 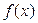 .
.
Найдём производную функции 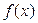 . Имеем
. Имеем
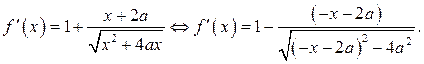
Оценим производную  .
.
Если 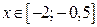 и
и 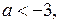 то
то 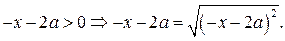 Очевидно,
Очевидно, 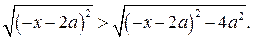 Тогда
Тогда
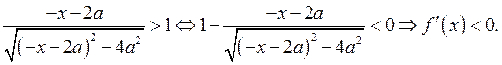
Так как 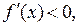 где
где 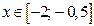 и
и 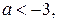 то функция
то функция 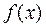 убывает на отрезке
убывает на отрезке 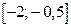 . Тогда
. Тогда 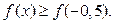
Если 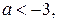 то
то 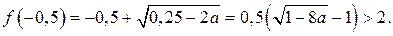
(Отметим, если 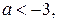 то
то 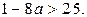 )
)
Таким образом, если 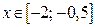 и
и 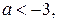 то
то 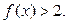
Ответ. 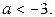
12. Найдите все значения х, при которых неравенство 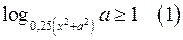 выполняется для всех значений параметра
выполняется для всех значений параметра 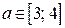 .
.
Решение. 1. Рассмотрим неравенство (1) при 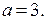 Имеем
Имеем
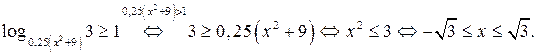
Искомые значения х могут принадлежать отрезку 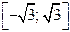 .
.
2. Рассмотрим неравенство (1) при 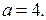 Имеем
Имеем
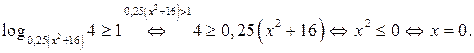
Очевидно: 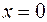 принадлежит отрезку
принадлежит отрезку 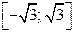 . Искомым значением возможен
. Искомым значением возможен 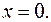
Проверим, будет ли выполняться неравенство (1) для всех 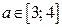 , если
, если 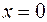 . Имеем
. Имеем
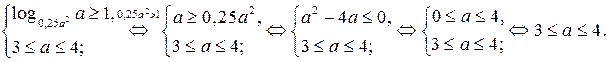 Ответ.
Ответ. 
13. Решите неравенство 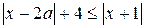 . (1)
. (1)
Решение. 1. Рассмотрим функции 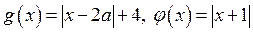 .
.
Графиком функции 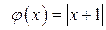 является «уголок» с вершиной в точке (–1;0) и со сторонами
является «уголок» с вершиной в точке (–1;0) и со сторонами 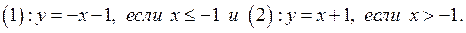
Графиком функции 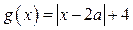 является «подвижный уголок» с вершиной в точке
является «подвижный уголок» с вершиной в точке 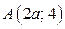 и со сторонами
и со сторонами
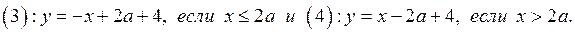
Отметим: для любого 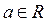 вершина «подвижного уголка» лежит на прямой
вершина «подвижного уголка» лежит на прямой 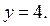
Исходное неравенство имеет решение тогда и только тогда, когда 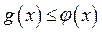 .
.
Замечание. Сторона (прямая) (1) «уголка» параллельна стороне (прямой) (3) «подвижного уголка», так же стороны (прямые) (2) и (4) параллельны.
2. Точки пересечения графика функции 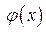 с прямой
с прямой 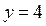 (ордината вершины «подвижного уголка» равна 4) найдём из уравнения
(ордината вершины «подвижного уголка» равна 4) найдём из уравнения
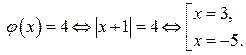
Ось абсцисс точками 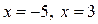 разбивается на 3 промежутка:
разбивается на 3 промежутка: 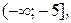 .
. 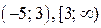
3. Рассмотрим следующие случаи.
1) Пусть 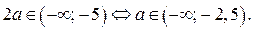
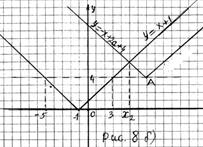
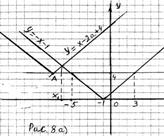 Из рисунка 8 а) следует: если
Из рисунка 8 а) следует: если 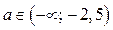 , то для любого
, то для любого 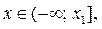 где
где 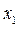 абсцисса точки пересечения прямых
абсцисса точки пересечения прямых 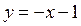 и
и 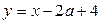 , выполняется неравенство
, выполняется неравенство 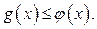 Тогда для
Тогда для 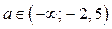 решениями неравенства (1) являются
решениями неравенства (1) являются 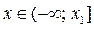 . Абсциссу
. Абсциссу 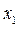 точки пересечения прямых
точки пересечения прямых 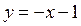 и
и 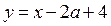 , где
, где 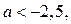 найдём из системы
найдём из системы
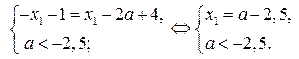
Если 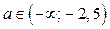 , то решениями неравенства (1) являются
, то решениями неравенства (1) являются 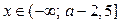 .
.
2) Если 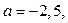 то часть прямой
то часть прямой 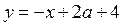 совпадает с частью прямой
совпадает с частью прямой 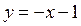 при
при 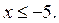 В этом случае решениями неравенства (1) являются
В этом случае решениями неравенства (1) являются 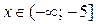 .
.
Из 1) и 2) следует, если 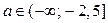 , то решениями неравенства (1) являются
, то решениями неравенства (1) являются 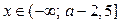 .
.
 3) Пусть
3) Пусть 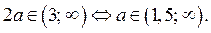
Из рисунка 8 б) следует: если 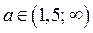 , то для любого
, то для любого 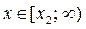 , где
, где 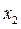 абсцисса точки пересечения прямых
абсцисса точки пересечения прямых 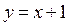 и
и 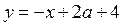 , выполняется неравенство
, выполняется неравенство 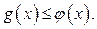 Тогда для
Тогда для 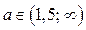 решениями неравенства (1) являются
решениями неравенства (1) являются 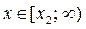 . Абсциссу
. Абсциссу 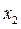 точки пересечения прямых
точки пересечения прямых 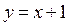 и
и 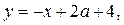 где
где 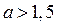 найдём из системы
найдём из системы
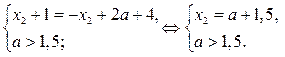
Итак, если 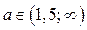 , то решениями неравенства (1) являются
, то решениями неравенства (1) являются 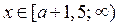
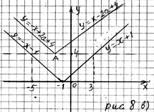 4) Если
4) Если 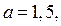 то часть прямой
то часть прямой 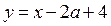 совпадает с частью прямой
совпадает с частью прямой 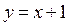 при
при 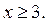 В этом случае решениями неравенства (1) являются
В этом случае решениями неравенства (1) являются 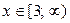 .
.
Из 3) и 4) следует, если 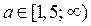 , то решениями неравенства (1) являются
, то решениями неравенства (1) являются 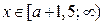 .
.
5) Пусть 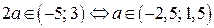 .
.
Из замечания и рисунка 8 в) следует, если 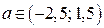 , то неравенство (1) не имеет решений, так как
, то неравенство (1) не имеет решений, так как 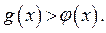
Ответ. Если 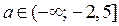 , то
, то 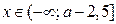 ; если
; если 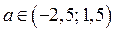 , то нет решений; если
, то нет решений; если 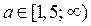 , то
, то 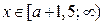 .
.
14. Решите неравенство 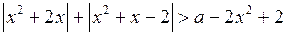 .
.
Решение. На координатной плоскости х0а построим множество точек, удовлетворяющих уравнению 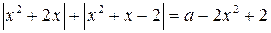 . (1)
. (1)
Для построения множества точек, удовлетворяющих уравнению (1), проделаем следующее.
1. Приравняем нулю выражения, стоящие под знаком модуля: 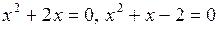 . Получим
. Получим 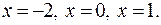
Построим прямые 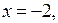
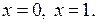 Эти прямые разобьют плоскость х0а на 4 области.
Эти прямые разобьют плоскость х0а на 4 области.
2. Рассмотрим уравнение (1) в каждой области и построим в каждой области соответствующее множество точек.
В области I уравнение (1) равносильно системе
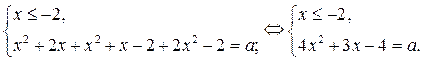
Имеем
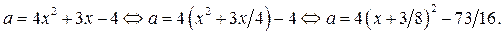
Замечание. Функция 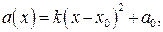 где
где 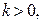 на промежутке
на промежутке 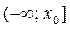 убывает, а на промежутке
убывает, а на промежутке 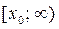 возрастает.
возрастает.
Графиком функции 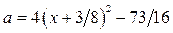 является парабола, ветви которой направлены вверх. Из замечания следует, что функция
является парабола, ветви которой направлены вверх. Из замечания следует, что функция  при
при 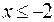 , убывает. Для построения части параболы найдём значение функции
, убывает. Для построения части параболы найдём значение функции 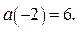 В области I строим часть параболы
В области I строим часть параболы 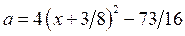 .
.
В области II уравнение (1) равносильно системе
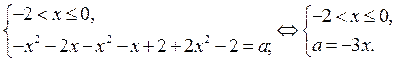
Графиком уравнения 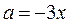 является прямая, которая в области II проходит через точки
является прямая, которая в области II проходит через точки 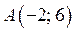 и
и 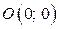 . В области II строим часть прямой
. В области II строим часть прямой 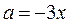 .
.
В области III уравнение (1) равносильно системе
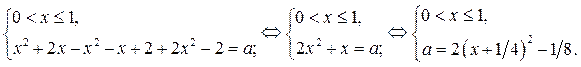
Графиком функции 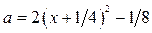 является парабола, ветви которой направлены вверх. Из замечания следует, что функция
является парабола, ветви которой направлены вверх. Из замечания следует, что функция 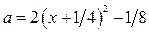 при
при 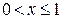 , возрастает. Для построения части параболы найдём значения функции:
, возрастает. Для построения части параболы найдём значения функции: 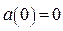 и
и 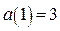 . В области III строим часть параболы
. В области III строим часть параболы 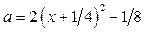 , которая проходит через точки
, которая проходит через точки 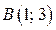 и
и 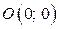 .
.
В области IV уравнение (1) равносильно системе
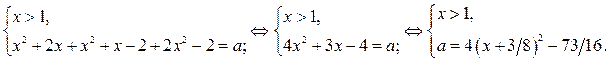 Графиком функции
Графиком функции 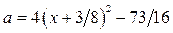 является парабола, ветви которой направлены вверх. Из замечания следует, что функция
является парабола, ветви которой направлены вверх. Из замечания следует, что функция  при
при 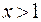 возрастает. Для построения части параболы найдём значение функции
возрастает. Для построения части параболы найдём значение функции 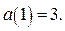 В области IV строим часть параболы
В области IV строим часть параболы 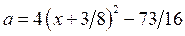 .
.
Замечание. Парабола 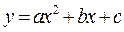 разбивает координатную плоскость на две области, в каждой из которых функция
разбивает координатную плоскость на две области, в каждой из которых функция 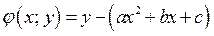 сохраняет знак.
сохраняет знак.
Дляопределения области, каждая точка которой принадлежит множеству решений неравенства 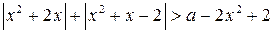 , возьмём любую точку плоскости х0а, например, точку (0; 1) и определим, удовлетворяет ли она рассматриваемому неравенству. Так как точка (0; 1) не удовлетворяет исходному неравенству, то множеством решений исходного неравенства является область, которой не принадлежит точка (0; 1). Заштрихованная область, в которую не входит граница области (рисунок 9), соответствует множеству решений исходного неравенства.
, возьмём любую точку плоскости х0а, например, точку (0; 1) и определим, удовлетворяет ли она рассматриваемому неравенству. Так как точка (0; 1) не удовлетворяет исходному неравенству, то множеством решений исходного неравенства является область, которой не принадлежит точка (0; 1). Заштрихованная область, в которую не входит граница области (рисунок 9), соответствует множеству решений исходного неравенства.
Для того чтобы найти решения исходного неравенства, проведём прямые 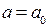 . Ось а прямыми
. Ось а прямыми 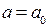 разбивается на 4 промежутка:
разбивается на 4 промежутка: 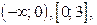
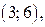
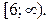 На каждом промежутке найдём решение исходного неравенства. Для этого на каждом промежутке из уравнения границы находим значения х, которые соответствуют концам отрезков прямой
На каждом промежутке найдём решение исходного неравенства. Для этого на каждом промежутке из уравнения границы находим значения х, которые соответствуют концам отрезков прямой 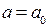 , попавшей в заштрихованную область.
, попавшей в заштрихованную область.
а) Если 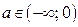 , то решениями исходного неравенства являются
, то решениями исходного неравенства являются 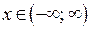 .
.
б) Если 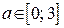 , то граница заштрихованной области задана уравнениями:
, то граница заштрихованной области задана уравнениями: 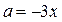 и
и 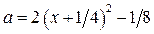 . Из первого уравнения находим
. Из первого уравнения находим 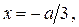 а из второго –
а из второго – 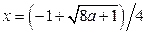 (берём больший корень уравнения
(берём больший корень уравнения 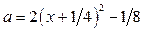 , так как
, так как 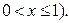 Решениями исходного неравенства являются
Решениями исходного неравенства являются 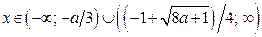 .
.
в) Если 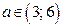 , то граница заштрихованной области задана уравнениями:
, то граница заштрихованной области задана уравнениями: 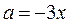 и
и 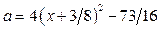 . Из первого уравнения находим
. Из первого уравнения находим 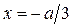 , а из второго –
, а из второго – 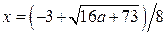 (берём больший корень уравнения
(берём больший корень уравнения 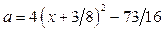 , так как
, так как 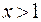 ).
). 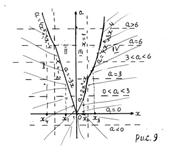 Решениями исходного неравенства являются
Решениями исходного неравенства являются 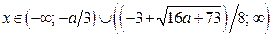 .
.
г) Если 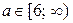 , то граница заштрихованной области задана уравнением
, то граница заштрихованной области задана уравнением 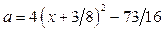 . Из этого уравнения находим:
. Из этого уравнения находим: 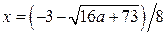 ,
, 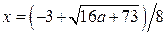 . Тогда решениями исходного неравенства являются
. Тогда решениями исходного неравенства являются 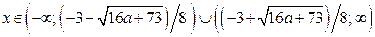 .
.
Ответ. Если 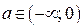 , то
, то 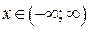 ;
;
если 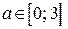 , то
, то 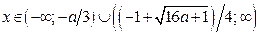 ;
;
если 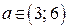 , то
, то 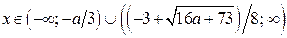 ;
;
если 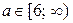 , то
, то 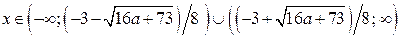 .
.
15. Решите неравенство 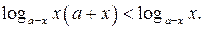
Решение. Запишем неравенство в виде 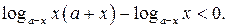
Рассмотрим функцию 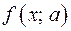
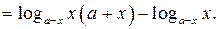
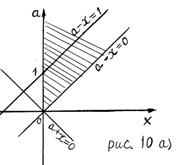
1. Область определения функции (ООФ) 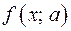 определяется системой неравенств
определяется системой неравенств
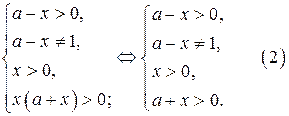
На координатной плоскости х0а построим прямые: 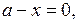
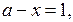
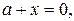
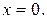
ООФ, то есть множество решений системы (2), изображено на рисунке 10а) штриховкой (прямые 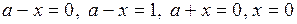 не принадлежит множеству решений системы (2)).
не принадлежит множеству решений системы (2)).
В ООФ имеем
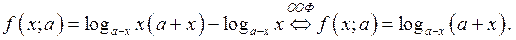
 2. Нули функции
2. Нули функции 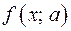 находим из уравнения
находим из уравнения
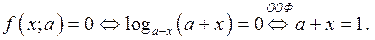
Нулями функции 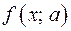 являются точки части прямой
являются точки части прямой 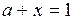 , принадлежащие ООФ.
, принадлежащие ООФ.
Строим часть прямой 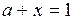 в заштрихованной области, то есть в области, являющейся ООФ (рис. 10б)). Точка
в заштрихованной области, то есть в области, являющейся ООФ (рис. 10б)). Точка 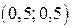 является точкой пересечения прямых
является точкой пересечения прямых 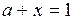 и
и 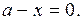
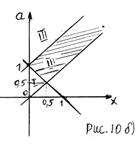 3. Определим знак функции
3. Определим знак функции 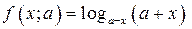 в областях: I (ограниченной прямыми
в областях: I (ограниченной прямыми 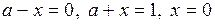 ),II (ограниченной прямыми
),II (ограниченной прямыми 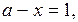
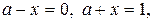 ), III (ограниченной прямыми
), III (ограниченной прямыми 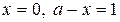 ).
).
Определим знак функции 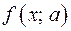 , например, в точке
, например, в точке 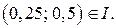 Имеем
Имеем 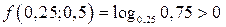 . Так как точка (0,25; 0,5) не удовлетворяет исходному неравенству, то область I не является множеством решений исходного неравенства.
. Так как точка (0,25; 0,5) не удовлетворяет исходному неравенству, то область I не является множеством решений исходного неравенства.
Так как при переходе через прямую 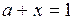 знак функции
знак функции 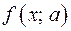 меняется на противоположный, то
меняется на противоположный, то 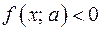 в области II. Это означает, что область II является множеством решений исходного неравенства.
в области II. Это означает, что область II является множеством решений исходного неравенства.
Так как при переходе через прямую 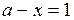 знак функции
знак функции 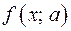 меняется на противоположный, то
меняется на противоположный, то 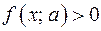 в области III. Это означает, что область III не является множеством решений исходного неравенства.
в области III. Это означает, что область III не является множеством решений исходного неравенства.
Для того чтобы найти решения исходного неравенства в области II проведём прямые 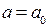 . Ось а прямыми
. Ось а прямыми 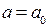 разбивается на 2 промежутка:
разбивается на 2 промежутка: 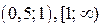 . На каждом промежутке найдём решение исходного неравенства. Для этого на каждом промежутке из уравнения границы находим значения х, которые соответствуют концам отрезков прямой
. На каждом промежутке найдём решение исходного неравенства. Для этого на каждом промежутке из уравнения границы находим значения х, которые соответствуют концам отрезков прямой 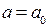 , попавшей в область II.
, попавшей в область II.
а) Если 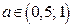 , то граница область II задана уравнениями:
, то граница область II задана уравнениями: 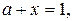
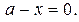 Из этих уравнений находим
Из этих уравнений находим 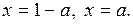
Решениями исходного неравенства, если 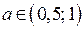 являются
являются 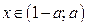 (отметим, что прямая
(отметим, что прямая 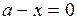 не принадлежит ООФ, и точки прямой
не принадлежит ООФ, и точки прямой 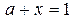 не принадлежат множеству решений исходного неравенства, так как это строгое неравенство).
не принадлежат множеству решений исходного неравенства, так как это строгое неравенство).
б) Если 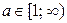 , то граница область II задана уравнениями:
, то граница область II задана уравнениями: 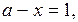
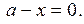 Из этих уравнений находим
Из этих уравнений находим 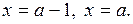
Решениями исходного неравенства, если 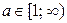 являются
являются 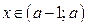 .
.
Ответ. Если 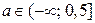 , то решений нет; если
, то решений нет; если 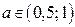 , то
, то 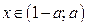 ; если
; если 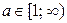 , то
, то 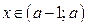 .
.
16. При всех значениях параметра 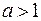 решите неравенство
решите неравенство
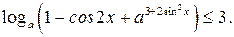
Решение. 1. Так как 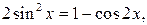 то сделаем замену
то сделаем замену 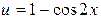 , где
, где 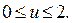 .
.
Исходное неравенство принимает вид 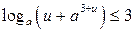 . (2)
. (2)
Так как 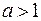 (по условию) и
(по условию) и 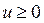 , то
, то
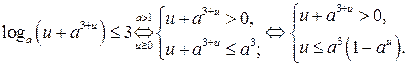
2.Рассмотрим второе неравенство последней системы.
Так как 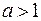 и
и 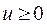 , то
, то 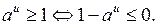 Тогда
Тогда
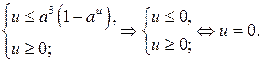
Таким образом, решением неравенства (2) является 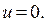
Решения исходного неравенства находим из уравнения 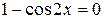 . Корни последнего уравнения:
. Корни последнего уравнения: 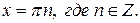
Ответ. 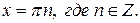
17. Найдите все значения параметра а, при которых множеством решений неравенства 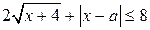 а) является отрезок; б) является отрезок длиной 4.
а) является отрезок; б) является отрезок длиной 4.
Решение. Сделаем замену 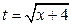 . Очевидно,
. Очевидно, 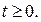 Тогда
Тогда 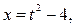 где
где 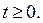 Исходное неравенство принимает вид
Исходное неравенство принимает вид 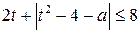 , где
, где 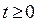 . Перепишем неравенство в виде
. Перепишем неравенство в виде 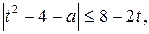 где
где 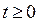 (1)
(1)
Замечание. Решением исходного неравенства и неравенства (1) является отрезок при одних и тех же значениях параметра а (так как 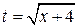 , то для каждого значения t находится единственное значение х).
, то для каждого значения t находится единственное значение х).
2.Рассмотрим неравенство 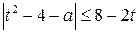 , где
, где 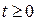 .Имеем
.Имеем
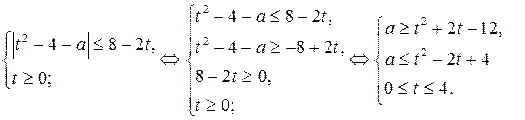
4. На координатной плоскости 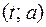 построим множество точек, удовлетворяющих системе уравнений
построим множество точек, удовлетворяющих системе уравнений
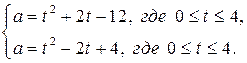
 а) Графиком функции
а) Графиком функции 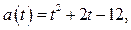 где
где 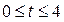 является часть параболы, ветви которой направлены вверх. Абсцисса вершины параболы
является часть параболы, ветви которой направлены вверх. Абсцисса вершины параболы 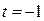 не принадлежит отрезку
не принадлежит отрезку 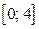 . Функция
. Функция 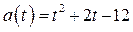 возрастает на отрезке
возрастает на отрезке 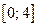 . Для построения части параболы найдём значения функции:
. Для построения части параболы найдём значения функции: 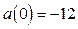 и
и 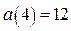 .
.
б) Графиком функции 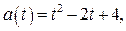 где
где 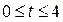 является часть параболы, ветви которой направлены вверх. Вершина параболы в точке
является часть параболы, ветви которой направлены вверх. Вершина параболы в точке 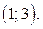 Абсцисса вершины параболы
Абсцисса вершины параболы 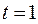 принадлежит отрезку
принадлежит отрезку 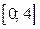 . Для построения части параболы найдём значения функции:
. Для построения части параболы найдём значения функции: 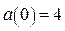 и
и 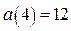 .
.
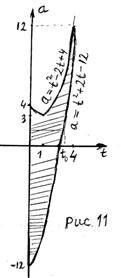
5. Множеством решений исходного неравенства является область, которой принадлежит точка (1; 0) (точка (1; 0) удовлетворяет неравенству 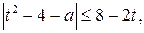 где
где 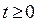 ). Заштрихованная область (рис. 11), в которую входит граница области:
). Заштрихованная область (рис. 11), в которую входит граница области: 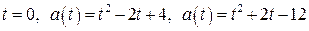 , является множеством решений неравенства (1).
, является множеством решений неравенства (1).
Из рисунка 11 следует: если 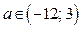 , то множеством решений неравенства (1), а значит и исходного неравенства (следует из замечания), является отрезок.
, то множеством решений неравенства (1), а значит и исходного неравенства (следует из замечания), является отрезок.
6. Найдём значения параметра а, при которых решением исходного неравенства является отрезок длиной 4.
Пусть множеством решений неравенства (1) является отрезок 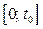 , где
, где 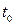 корень уравнения
корень уравнения 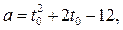 где
где 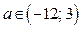 . Выразим
. Выразим 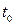 через а. Имеем
через а. Имеем
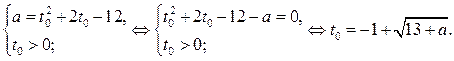
Решением неравенства (1) является отрезок 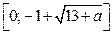 , где
, где 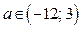 .
.
Перейдём к переменой х. Тогда решением исходного неравенства является отрезок 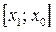 . Так как
. Так как 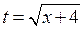 , то
, то 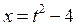 .
.
Если 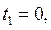 то
то 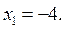
Если 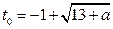 , то
, то 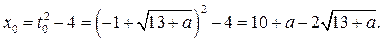
Итак, 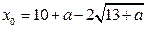 , где
, где 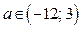 .
.
Длина отрезка 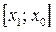 равна 4 тогда и только тогда, когда
равна 4 тогда и только тогда, когда
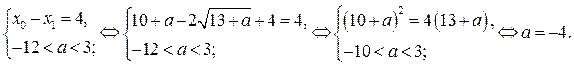
Ответ. 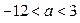 ;
; 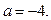
18. Найдите все значения параметра а, при каждом из которых множеством решений неравенства 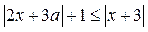 является отрезок длиной больше 3, но меньше 5.
является отрезок длиной больше 3, но меньше 5.
Решение. 1. Имеем
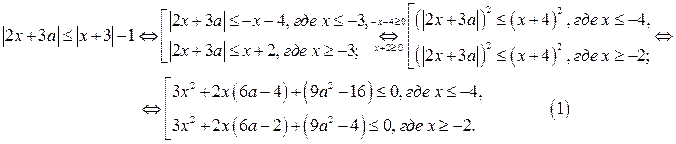 1) Рассмотрим первое неравенство совокупности (1).
1) Рассмотрим первое неравенство совокупности (1).
Решением неравенства является отрезок, если оба корня уравнения, 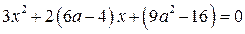 , где
, где 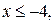 (2) не больше числа
(2) не больше числа 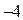 .
.
Замечание. Квадратное уравнение 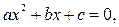 где
где 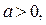 имеет два корня, которые не больше (не меньше) числа
имеет два корня, которые не больше (не меньше) числа 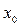 тогда и только, когда
тогда и только, когда 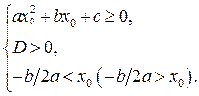
Найдём дискриминант уравнения (2). Имеем
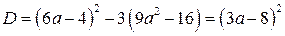
Из замечания следует: уравнение (2) имеет два корня, которые не больше числа 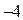 тогда и только, когда
тогда и только, когда
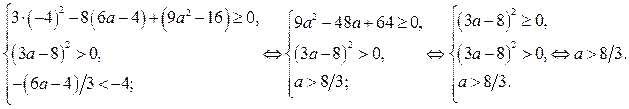 Итак, если
Итак, если 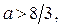 то уравнение (2) имеет два корня
то уравнение (2) имеет два корня 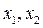 , которые не больше числа
, которые не больше числа 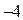 .
.
Так как 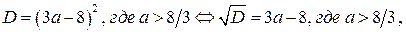 то
то
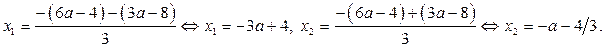 Решением неравенства
Решением неравенства 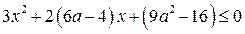 , где
, где 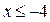 и
и 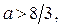 а
а
значит и исходного неравенства, является отрезок 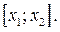
2) Рассмотрим второе неравенство совокупности (2).
Решением неравенства является отрезок, если оба корня уравнения, 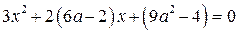 , где
, где 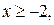 (3) не меньше числа
(3) не меньше числа 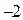 .
.
Найдём дискриминант уравнения (3). Имеем
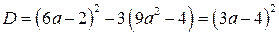
Из замечания следует: уравнение (3) имеет два корня, которые не меньше числа 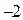 тогда и только, когда
тогда и только, когда
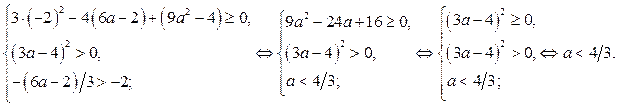 Итак, если
Итак, если 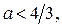 то уравнение (3) имеет два корня
то уравнение (3) имеет два корня 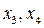 , которые не меньше числа
, которые не меньше числа 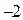 .
.
Так как 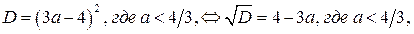 то
то
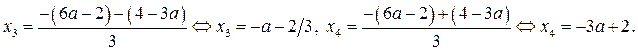 Решением неравенства
Решением неравенства 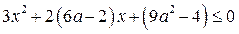 , где
, где 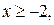
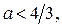 а значит и исходного неравенства, является отрезок
а значит и исходного неравенства, является отрезок 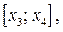 где
где 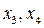 корни уравнения (3).
корни уравнения (3).
Из 1) и 2) следует, что множеством решений исходного неравенства является отрезок 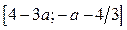 , если
, если 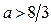 или отрезок
или отрезок 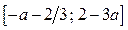 , если
, если 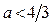 .
.
2. Найдём значения параметра а, при которых решением исходного неравенства является отрезок длиной больше 3, но меньше 5.
а) Длина отрезка 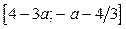 , если
, если 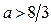 , больше 3, но меньше 5 тогда и только тогда, когда
, больше 3, но меньше 5 тогда и только тогда, когда
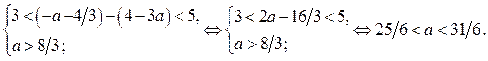
б) Длина отрезка 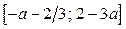 , если
, если 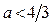 , больше 3, но меньше 5 тогда и только тогда, когда
, больше 3, но меньше 5 тогда и только тогда, когда
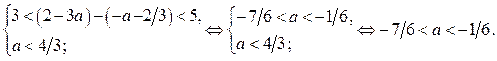
Ответ.  .
.
19. Найти все значения параметра а, при которых число целы
 2015-03-22
2015-03-22 589
589








