- Пусть функция
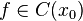 непрерывна в
непрерывна в 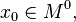 и существуют конечные или бесконечные односторонние производные
и существуют конечные или бесконечные односторонние производные 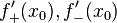 . Тогда при условии
. Тогда при условии
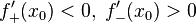
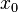 является точкой строгого локального максимума. А если
является точкой строгого локального максимума. А если
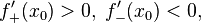
то 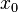 является точкой строгого локального минимума.
является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке 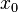 .
.
- Пусть функция
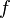 непрерывна и дважды дифференцируема в точке
непрерывна и дважды дифференцируема в точке 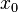 . Тогда при условии
. Тогда при условии
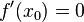 и
и 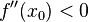
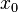 является точкой локального максимума. А если
является точкой локального максимума. А если
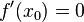 и
и 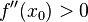
то 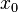 является точкой локального минимума.
является точкой локального минимума.
- Пусть функция
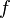 дифференцируема
дифференцируема 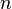 раз в точке
раз в точке 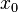 и
и 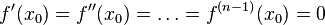 , а
, а 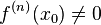 .
.
Если 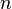 чётно и
чётно и 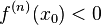 , то
, то 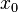 - точка локального максимума. Если
- точка локального максимума. Если 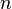 чётно и
чётно и 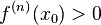 , то
, то 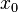 - точка локального минимума. Если
- точка локального минимума. Если 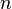 нечётно, то экстремума нет.
нечётно, то экстремума нет.
49. Условия выпуклости и вогнутости графиков функций.
График функции y = f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y = f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
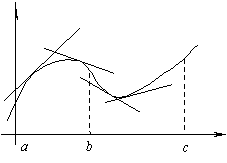
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Примеры.
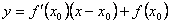 . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной. . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
|   
|
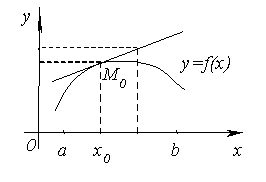
Итак, уравнение кривой имеет вид y = f(x). Обозначим 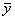 ординату касательной, соответствующую абсциссе x. Тогда
ординату касательной, соответствующую абсциссе x. Тогда 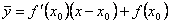 . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет
. Следовательно, разность ординат кривой и касательной при одном и том же значении x будет 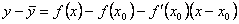 .
.
Разность f(x) – f(x0) преобразуем по теореме Лагранжа 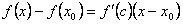 , где c между x и x0.
, где c между x и x0.
Таким образом,
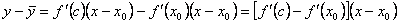 .
.
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: 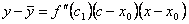 , где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
, где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
- Предположим, что x > x 0. Тогда x0 < c1 < c < x, следовательно,
 (x – x 0) > 0 и (c – x 0) > 0. Поэтому
(x – x 0) > 0 и (c – x 0) > 0. Поэтому 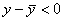 .
. - Пусть x < x0, следовательно, x < c < c 1 < x 0 и (x – x 0) < 0, (c – x 0) < 0. Поэтому вновь
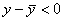 .
.
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
- See more at: https://www.toehelp.ru/theory/math/lecture10/lecture10.html#sthash.Znvd5lmX.dpuf
50. Точки перегиба и достаточные условия их существования.
Точка перегиба функции — это точка, в которой функция непрерывна и при переходе через которую функция меняет направление выпуклости.
Необходимое условие существования точки перегиба: если функция 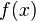 дважды дифференцируемая в некоторой выколотой окрестности точки
дважды дифференцируемая в некоторой выколотой окрестности точки 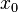 , то
, то 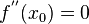 или
или 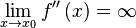 .
.
Достаточное условие существования точки перегиба: если функция 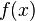 в некоторой окрестности точки
в некоторой окрестности точки 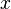
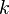 раз непрерывно дифференцируема, причем
раз непрерывно дифференцируема, причем 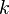 нечётно и
нечётно и 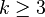 , и
, и 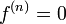 при
при 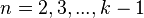 , а
, а 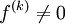 , то функция
, то функция 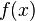 имеет в
имеет в 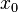 точку перегиба.
точку перегиба.
51. Асимптоты и алгоритмы их изыскания.
Аси́мпто́та [2] (от греч.ασϋμπτωτος — несовпадающий, не касающийся кривой сбесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямойстремится к нулю при удалении точки вдоль ветви вбесконечность[3].
52. Общая схема исследования функций.
При исследовании функций и построении их графиков целесообразно пользоваться следующей схемой.
1. Нахождение области определения функции.
2. Исследование функции на четность и нечетность.
3. Установление области непрерывности функции и точек разрыва. Отыскание вертикальных асимптот.
4. Исследование поведения функции при 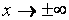 (если она там определена). Отыскание горизонтальных и наклонных асимптот.
(если она там определена). Отыскание горизонтальных и наклонных асимптот.
5. Нахождение экстремумов и интервалов монотонности функции. Составление таблицы.
6. Нахождение интервалов выпуклости и вогнутости и точек перегиба графика функции.
7. Нахождение точек пересечения графика функции с осями, интервалов знакопостоянства функции. Составление таблицы. Отыскание дополнительных точек для построения графика.
8. Построение графика функции.
 2015-03-22
2015-03-22 549
549

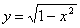 выпукла на [–1; 1].
выпукла на [–1; 1].






