Теорема Ролля

Теорема

Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)

Пусть функция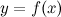

1. непрерывна на отрезке ;
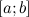2. дифференцируема на интервале ;
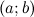3. на концах отрезка 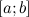принимает равные значения .

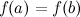Тогда на интервале 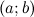найдется, по крайней мере, одна точка 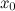, в которой .

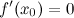Следствие. (Геометрический смысл теоремы Ролля)

Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.

Следствие.

Если 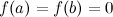, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.