Теорема

Теорема Лагранжа. (О конечных приращениях)

Пусть функция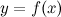

1. непрерывна на отрезке ;
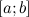2. дифференцируема на интервале .

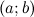Тогда на интервале 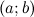найдется по крайней мере одна точка 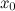, такая, что

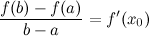
44. Правила Лопиталя- Бернулли.

Теорема Лопита́ля (также правило Бернулли — Лопиталя ^[1]) — метод нахождения пределов функций, раскрывающий неопределённости вида 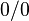и 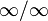. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Теорема Лопиталя:

Если:

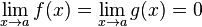1. или ;
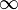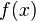2. и 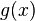дифференцируемы в окрестности ;
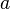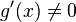3. в окрестности ;
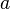4. существует ,

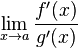то существует .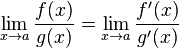

Пределы также могут быть односторонними.

45. Формула Тейлора для вещественных функций одной вещественной переменной.

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.

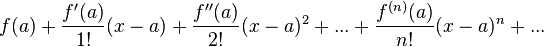
46. Применение формулы Тейлора для приближенного вычисления элементарных функций.

47. Условия монотонности функции, экстремумы функции (локальные и глобальные).

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданноммножестве.

48. Необходимые и достаточные условия существования экстремумов.