Рассмотрим следующую модель.
Игроки А и В играют с нулевой суммой.
Стратегии игрока А: А 1, А 2,…, Аn.
Стратегии игрока В: В 1, В 2,…, Вm.
Составим платежную матрицу игры для игрока А:
| В 1 | В 2 | … | Вn | |
| А 1 | a 11 | a 12 | … | a 1 n |
| А 2 | a 21 | a 21 | … | a 2 n |
| … | … | |||
| Аm | an 1 | an 2 | … | Amn |
Оптимальной стратегией игрока в матричной игре называется такая, которая обеспечивает ему максимальный выигрыш.
Игрок А, выбирая свою стратегию Аi, понимает, что В ответит ему такой стратегией Вj, чтобы выигрыш А был минимальным.
Поэтому, из всех наихудших вариантов (минимальных элементов каждой строки платежной матрицы) 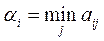 , игроку А выгодно выбрать стратегию, соответствующую максимальному из этих элементов:
, игроку А выгодно выбрать стратегию, соответствующую максимальному из этих элементов:
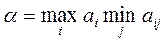
Величина a называется нижней ценой игры или максимином.
Это гарантированный выигрыш игрока А.
С другой стороны, игрок В выбирая свою стратегию В j понимает, что игрок А ответит такой стратегией Аi, чтобы его выигрыш был максимален. Поэтому из наилучших вариантов для А (максимальных элементов каждого столбца) 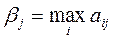 игроку В рационально выбрать свою стратегию, соответствующую минимальному из этих чисел:
игроку В рационально выбрать свою стратегию, соответствующую минимальному из этих чисел:
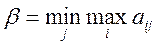
Величина β называется верхней ценой игры или минимаксом.
Это максимальный проигрыш игрока В.
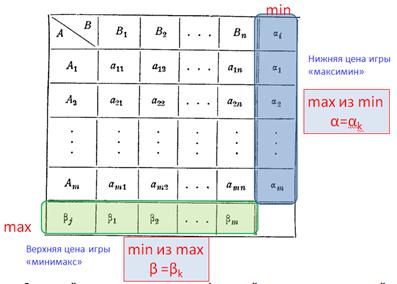
Реальный результат решения конфликтной ситуации, называемый ценой игры ν, заключен между верхней и нижней ценой: α≤ ν ≤ β
В случае, если верхняя и нижняя цены совпадают α=β=ν, то игра имеет решение в чистых стратегиях
В геометрии точку на поверхности, обладающую аналогичным свойством (одновременный минимум по одной координате и максимум по другой), называют седловой точкой; по аналогии этот термин применяется и в теории игр.
Элемент матрицы, обладающий этим свойством, называется седловой точкой матрицы, а про игру говорят, что она имеет седловую точку.
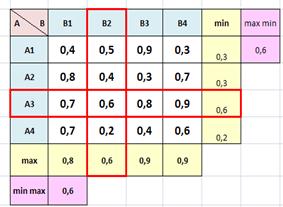
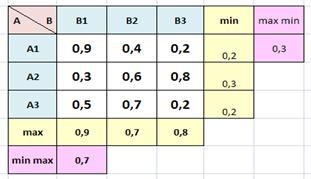
Пример:
| 
|
| Игра с седловой точкой 0,6 | Игра без седловой точки |
 2015-03-22
2015-03-22 555
555








