Лекция 14.
Закон больших чисел не исследует вид предельного закона распределения суммы случайных величин. Этот вопрос рассмотрен в группе теорем, называемых центральной предельной теоремой. Они утверждают, что закон распределения суммы случайных величин, каждая из которых может иметь различные распределения, приближается к нормальному при достаточ-но большом числе слагаемых. Этим объясняется важность нормального закона для практичес-ких приложений.
Характеристические функции.
Для доказательства центральной предельной теоремы используется метод характеристичес-ких функций.
Определение 14.1. Характеристической функцией случайной величины Х называется функция
g (t) = M (eitX) (14.1)
Таким образом, g (t) представляет собой математическое ожидание некоторой комплексной случайной величины U = eitX, связанной с величиной Х. В частности, если Х – дискретная случайная величина, заданная рядом распределения, то
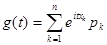 . (14.2)
. (14.2)
Для непрерывной случайной величины с плотностью распределения f (x)
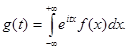 (14.3)
(14.3)
Пример 1. Пусть Х – число выпадений 6 очков при одном броске игральной кости. Тогда по формуле (14.2) g (t) = 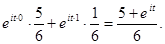
Пример 2. Найдем характеристическую функцию для нормированной непрерывной случайной величины, распределенной по нормальному закону 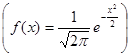 . По формуле (14.3)
. По формуле (14.3) 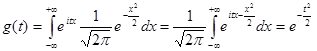 (использовалась формула
(использовалась формула 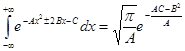 и то, что i ² = -1).
и то, что i ² = -1).
Свойства характеристических функций.
1. Функцию f (x) можно найти по известной функции g (t) по формуле
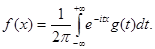 (14.4)
(14.4)
(преобразование (14.3) называется преобразованием Фурье, а преобразование (14.4) – обратным преобразованием Фурье).
2. Если случайные величины Х и Y связаны соотношением Y = aX, то их характеристические функции связаны соотношением
gy (t) = gx (at). (14.5)
3. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых: для 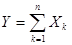
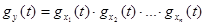 (14.6)
(14.6)
Теорема 14.1 (центральная предельная теорема для одинаково распределенных слагае-мых). Если Х 1, Х 2,…, Хп,… - независимые случайные величины с одинаковым законом распределения, математическим ожиданием т и дисперсией σ 2, то при неограниченном увеличении п закон распределения суммы 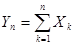 неограниченно приближается к нор-мальному.
неограниченно приближается к нор-мальному.
Доказательство.
Докажем теорему для непрерывных случайных величин Х 1, Х 2,…, Хп (доказательство для дискретных величин аналогично). Согласно условию теоремы, характеристические функции слагаемых одинаковы: 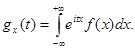 Тогда по свойству 3 характеристическая функция суммы Yn будет
Тогда по свойству 3 характеристическая функция суммы Yn будет 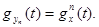 Разложим функцию gx (t) в ряд Маклорена:
Разложим функцию gx (t) в ряд Маклорена:
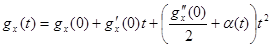 , где
, где 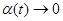 при
при 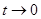 .
.
Найдем 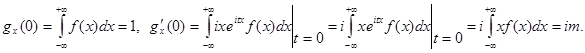
Если предположить, что т = 0 (то есть перенести начало отсчета в точку т), то 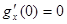 .
.
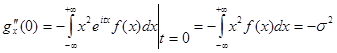 (так как т = 0). Подставив полученные результаты в формулу Маклорена, найдем, что
(так как т = 0). Подставив полученные результаты в формулу Маклорена, найдем, что
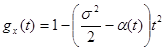 .
.
Рассмотрим новую случайную величину 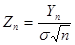 , отличающуюся от Yn тем, что ее дисперсия при любом п равна 0. Так как Yn и Zn связаны линейной зависимостью, достаточно доказать, что Zn распределена по нормальному закону, или, что то же самое, что ее характе-ристическая функция приближается к характеристической функции нормального закона (см. пример 2). По свойству характеристических функций
, отличающуюся от Yn тем, что ее дисперсия при любом п равна 0. Так как Yn и Zn связаны линейной зависимостью, достаточно доказать, что Zn распределена по нормальному закону, или, что то же самое, что ее характе-ристическая функция приближается к характеристической функции нормального закона (см. пример 2). По свойству характеристических функций
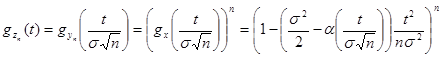 .
.
Прологарифмируем полученное выражение:
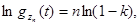 где
где 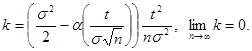
Разложим 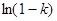 в ряд при п → ∞, ограничившись двумя членами разложения, тогда ln(1 - k) ≈ - k. Отсюда
в ряд при п → ∞, ограничившись двумя членами разложения, тогда ln(1 - k) ≈ - k. Отсюда
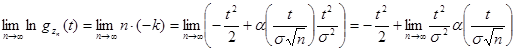 , где последний предел равен 0, так как
, где последний предел равен 0, так как 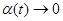 при
при 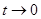 . Следовательно,
. Следовательно, 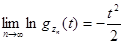 , то есть
, то есть 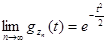 - характеристическая функция нормального распределения. Итак, при неограниченном увеличении числа слагаемых характеристическая функция величины Zn неограниченно приближается к характеристической функции нормального закона; следова-тельно, закон распределения Zn (и Yn) неограниченно приближается к нормальному. Теорема доказана.
- характеристическая функция нормального распределения. Итак, при неограниченном увеличении числа слагаемых характеристическая функция величины Zn неограниченно приближается к характеристической функции нормального закона; следова-тельно, закон распределения Zn (и Yn) неограниченно приближается к нормальному. Теорема доказана.
А.М.Ляпунов доказал центральную предельную теорему для условий более общего вида:
Теорема 14.2 (теорема Ляпунова). Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, для которых выполнено условие:
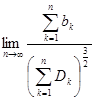 , (14.7)
, (14.7)
где bk – третий абсолютный центральный момент величины Хк, а Dk – ее дисперсия, то Х имеет распределение, близкое к нормальному (условие Ляпунова означает, что влияние каждого слагаемого на сумму ничтожно мало).
Практически можно использовать центральную предельную теорему при достаточно небольшом количестве слагаемых, так как вероятностные расчеты требуют сравнительно малой точности. Опыт показывает, что для суммы даже десяти и менее слагаемых закон их распределения можно заменить нормальным.
Частным случаем центральной предельной теоремы для дискретных случайных величин является теорема Муавра-Лапласа.
Теорема 14.3 (теорема Муавра-Лапласа). Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение:
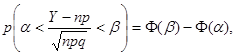 (14.8)
(14.8)
где Y – число появлений события А в п опытах, q = 1 – p.
Доказательство.
Будем считать, что 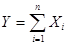 , где Хi – число появлений события А в i -м опыте. Тогда случай-ную величину
, где Хi – число появлений события А в i -м опыте. Тогда случай-ную величину 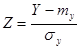 (см. теорему 14.1) можно считать распределенной по нормальному закону и нормированной, следовательно, вероятность ее попадания в интервал (α, β) можно найти по формуле
(см. теорему 14.1) можно считать распределенной по нормальному закону и нормированной, следовательно, вероятность ее попадания в интервал (α, β) можно найти по формуле
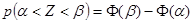 .
.
Поскольку Y имеет биномиальное распределение, 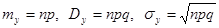 . Тогда
. Тогда 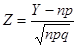 . Подставляя это выражение в предыдущую формулу, получим равенство (14.8).
. Подставляя это выражение в предыдущую формулу, получим равенство (14.8).
Следствие.
В условиях теоремы Муавра-Лапласа вероятность 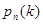 того, что событие А появится в п опытах ровно k раз, при большом количестве опытов можно найти по формуле:
того, что событие А появится в п опытах ровно k раз, при большом количестве опытов можно найти по формуле:
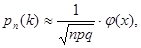 (14.9)
(14.9)
где 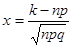 , а
, а 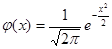 (значения этой функции приводятся в специальных таблицах).
(значения этой функции приводятся в специальных таблицах).
Пример 3. Найти вероятность того, что при 100 бросках монеты число выпадений герба окажется в пределах от 40 до 60.
Применим формулу (14.8), учитывая, что п = 0,5. Тогда пр = 100·0,5 = 50, 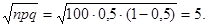 Тогда, если
Тогда, если 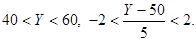 Следовательно,
Следовательно,
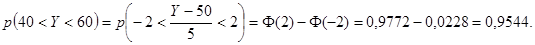
Пример 4. В условиях предыдущего примера найти вероятность того, что выпадет 45 гербов.
Найдем 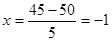 , тогда
, тогда 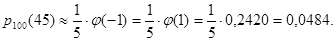
 2014-02-12
2014-02-12 8067
8067
