Формула Симпсона (параболических трапеций)

Вершины трех соседних точек соединяются дугой квадратной параболы.

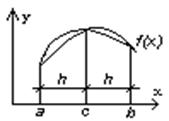Формула площади параболической трапеций

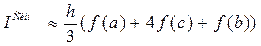, где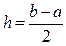

Промежуток интегрирования [a, b] делим точками x_1, x_2, ..., x_2n-1 на 2 n равных частей;

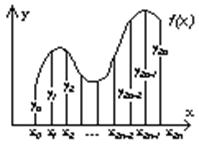длина каждой 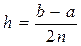(3.9)

Т.е. координаты узловых точек промежутков

x₀ = a,

x_i = a + i h, i = 0,1,..., 2n - 1, (3.10)

x_2n = b

Соответственно, значения подынтегральной функции в этих точках

y ₀ = f (x₀),

y _i = f (x_i),..., i = 0,1,..., 2n - 1, (3.11)

y _2n = f (x_2n).

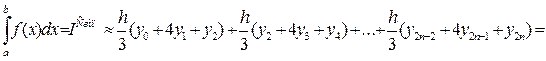
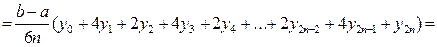
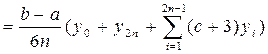, (3.12)

где с = .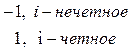

Формула (3.12) дает точные результаты для полиномов не выше 3-ей степени.

Предельная абсолютная погрешность 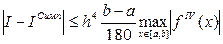(3.13)

Рекомендации по выполнению задания