Соответствие – способ задания взаимосвязей между элементами множества. Частными случаями соответствий являются функции, отображения, преобразования, отношения.
Пусть имеются два множества А и В. Элементы этих множеств могут сопоставляться друг другу, образуя пары (a, b). Если способ сопоставления определен, то говорят, что между множествами A и B установлено соответствие. При этом не обязательно, чтобы в соответствии участвовали все элементы множеств А и В.
Таким образом, чтобы задать соответствие надо задать:
1) множество A;
2) множество B;
3) множество 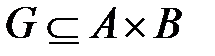 , определяющее правило соответствия, т. е. перечисляющее все пары (a, b), для которых справедливо соответствие.
, определяющее правило соответствия, т. е. перечисляющее все пары (a, b), для которых справедливо соответствие.
Записывается соответствие так:
g = (A, B, G)
Множество A называется о бластью отправления соответствия, множество B – областью прибытия соответствия, G – называется графиком соответствия.
Обычно соответствие обозначается символом графика соответствия, в нашем случае обозначим соответствие G.
С соответствием связаны еще два понятия. Область определения соответствия G – элементы множества A, участвующие в соответствии, обозначается эта область как пр1 G = { а:(a, b)  G }, и область значений соответствия G – элементы множества B, участвующие в соответствии, обозначается она как пр2 G = { b:{ а, b)
G }, и область значений соответствия G – элементы множества B, участвующие в соответствии, обозначается она как пр2 G = { b:{ а, b)  G }(рис. 4.1 и рис. 4.2).
G }(рис. 4.1 и рис. 4.2).
Если (а, b)  G,то говорят, что "b соответствует а при соответствии G ". Геометрически это обозначается стрелками (рис. 4.2).
G,то говорят, что "b соответствует а при соответствии G ". Геометрически это обозначается стрелками (рис. 4.2).
Пусть имеем множества A = {1, 2}, B = {3, 5}. Допустим элементы этих множеств образуют такие пары:
A  B = {(1, 3), (1, 5), (2, 3), (2, 5)}.
B = {(1, 3), (1, 5), (2, 3), (2, 5)}.
Из приведенных пар можно составить несколько соответствий, например, такие: G 1 = {(1, 3)}. Для этого соответствия Пр1 G 1 = {1}; Пр2 G 1 = {3}. G 2 = {(1, 3), (1, 5)}. Здесь Пр1 G 2 = {1}; Пр2 G 2 = {3, 5}.
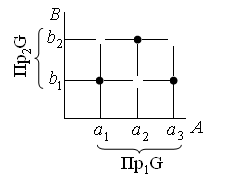
Рисунок 4.1 – График соответствия G
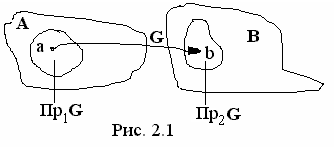
Рисунок 4.2 – Геометрическое представление соответствия G
Перечислим свойства соответствий.
соответствие всюду (полностью) определенно, если пр1 G = A. Частично определенное соответствие – в противном случае.
соответствие сюръективно, если пр2 G = В.
Образом элемента а  А в множестве В при соответствии G называется множество всех b
А в множестве В при соответствии G называется множество всех b  В,соответствующих элементу а
В,соответствующих элементу а  А.
А.
Прообразом элемента b в множестве А при соответствии G называется множество всех а  А,которым соответствует b
А,которым соответствует b  В.
В.
Образом множества 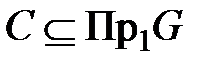 называется объединение образов всех элементов а
называется объединение образов всех элементов а  С.
С.
Прообразом множества 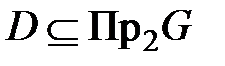 называется объединение прообразов всех элементов b
называется объединение прообразов всех элементов b  D.
D.
соответствие называется однозначным или функциональным, если образом любого элемента а из области определения пр1 G является единственный элемент b из области значений пр2 G.
Взаимно однозначное соответствие, при котором любой элемент множества A, участвующий в соответствии, имеет единственный образ в множестве B и наоборот, любой элемент множества B, участвующий в соответствии, имеет единственный прообраз в множестве A, называется инъективным.
Соответствие, которое всюду определено, сюръективно и инъективно называется биекцией.
Если между множествами А и В существует взаимно однозначное соответствие, то мощности этих множеств равны, т.е. | А| = | В|. В таком случае говорят, что множества A и В равномощны.
Множества, равномощные множеству натуральных чисел N,называются счетными. Множества, равномощные множеству вещественных чисел R, называются континуальными.
Пусть дано соответствие 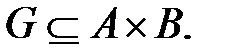 Тогда соответствие G –1
Тогда соответствие G –1 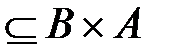 называется обратным к G,если G –1таково, что (b, а)
называется обратным к G,если G –1таково, что (b, а)  G –1 тогда и только тогда, когда (а, b)
G –1 тогда и только тогда, когда (а, b)  G. обратное соответствие обозначается:
G. обратное соответствие обозначается:
g –1 = (B, A, G –1)
где G –1 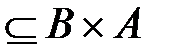 (не всегда
(не всегда 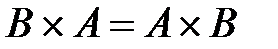 ).
).
Геометрически представление обратного соответствия получается из обозначения прямого соответствия заменой направления стрелок. Отсюда следует, что обратное соответствие обратного соответствия будет прямым, т.е.
(g –1)–1 = g.
Последовательное применение двух соответствий называется композицией соответствий.
Композиция соответствий есть операция с тремя множествами A, B, C, на которых определены два соответствия:
g = (A, B, G), 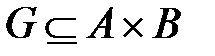 ,
,
p = (B, C, P), 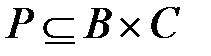 ,
,
причем область значений первого соответствия совпадает с областью определения второго:
Пр2 G = Пр1 P.
Первое соответствие определяет для любого 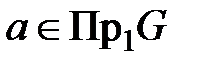 некоторый (возможно не один) элемент
некоторый (возможно не один) элемент 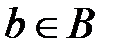 . В соответствии с определением композиции для этого b надо найти
. В соответствии с определением композиции для этого b надо найти 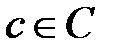 по второму правилу. В результате для
по второму правилу. В результате для 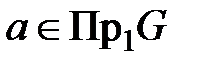 найдем
найдем 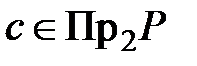 .
.
Композицию соответствий g и p обозначают g (p) или g 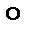 p, или просто gp.
p, или просто gp.
График композиции соответствий обозначают G 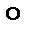 P.
P.
При этом приведенная выше композиция соответствий запишется так
g (p) = (A, C, G 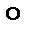 P), G
P), G 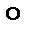 P
P 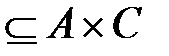 .
.
Операцию композиции можно распространить и на большее число (более двух) соответствий.
Композиция ассоциативна:
h (gp) = (hg) p
Но не коммутативна:
gp 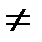 pg
pg
Даже если рассматриваются соответствия элементов на одном множестве.
 2015-03-22
2015-03-22 1555
1555
