Отношения – один из способов задания взаимосвязей между элементами множеств. Чаще всего используются унарные и бинарные отношения.
Унарные (одноместные) отношения отражают наличие какого–то определенного признака R (свойства и т.п.) у элементов множества М (например, "быть четным" на множестве натуральных чисел). Тогда все такие элементы а из множества М,которые отличаются данным признаком R,образуют некоторое подмножество в М, называемое унарным отношением R,т.е. 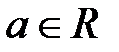 и
и 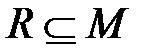 .
.
Бинарные (двухместные) отношения используются для определения каких–то взаимосвязей между парами элементов множества М (так, на множестве людей могут быть заданы, например, следующие бинарные отношения: "жить в одном городе", "быть моложе", "быть сыном", "работать в одной организации" и т.п.). Тогда все пары (а, b)элементов из М,между которыми имеет место данное отношение R,образуют подмножество пар из множества всех возможных пар элементов 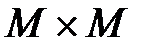 = М 2,называемое бинарным отношением R,т.е.
= М 2,называемое бинарным отношением R,т.е. 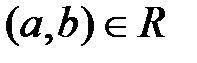 ,при этом
,при этом 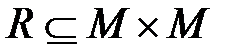 .
.
В общем случае могут рассматриваться п–местные (n–арные) отношения,например отношения между тройками элементов – трехместные (тернарные) отношения и т.д.
Вот пример тернарного отношения “образовывать сумму” x + y = z и отношения для четверок –“находиться в отношении пропорциональности” x / y = z / v.
Под п–местным отношением понимают подмножество R прямого произведения п множеств: 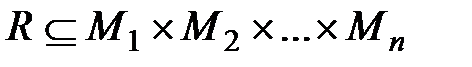 .
.
Говорят, что элементы а 1, а 2,..., аn 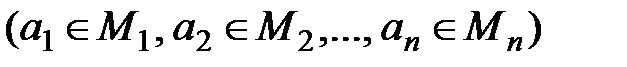 находятся в отношении R,если
находятся в отношении R,если 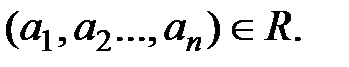
Если n –местное отношение R задано на множестве М, т.е.
M 1 = M 2 =…= Mn = М, то 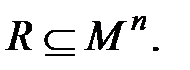
Рассмотрим детально бинарные отношения.
Итак, двухместным, или бинарным,отношением R называется подмножество пар 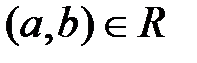 прямого произведения
прямого произведения 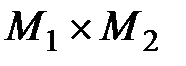 ,т.е.
,т.е. 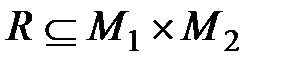 . При этом по аналогии с соответствиями множество М 1называют областью отправления отношения R,множество М 2 – областью прибытия. Часто рассматривают отношения R между парами элементов одного и того же множества М,тогда
. При этом по аналогии с соответствиями множество М 1называют областью отправления отношения R,множество М 2 – областью прибытия. Часто рассматривают отношения R между парами элементов одного и того же множества М,тогда 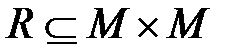 . Если а и b находятся в отношении R, это записывается как аRb.
. Если а и b находятся в отношении R, это записывается как аRb.
С отношениями связаны еще два понятия:
1) область определения D (R) и
2) область значений Q (R),
Эти понятия определяются соответственно, как 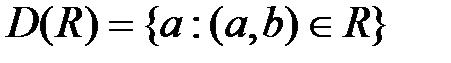 и
и 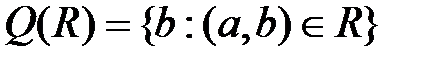 .
.
На рис. 6.1 приведен условный пример отношения 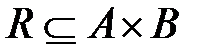 .
.
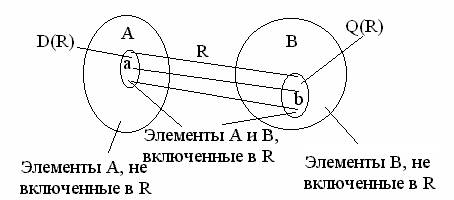
Рисунок 6.1 – Пример отношения R
Для задания бинарных отношенийгодятся любые способы задания множеств, так как отношения это подмножества некоторых множеств – прямых произведений двух множеств.
Отношения, определенные на конечных множествах, обычно задаются списком (перечислением) пар,для которых это отношение выполняется. Например, R = {(а, b), (а, с), (b, d)}.
Кроме такого представления, заимствованного у множеств, для отношений применяют также представление в виде матриц и графов.
Бинарному отношению 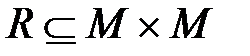 ,где M = { а 1, а 2,..., ап }, соответствует квадратная матрица порядка п,в которой элемент cij, стоящий на пересечении i– ойстроки и j –ого столбца, равен 1, если между элементами ai и аj имеет место отношение R,или 0, если оно отсутствует:
,где M = { а 1, а 2,..., ап }, соответствует квадратная матрица порядка п,в которой элемент cij, стоящий на пересечении i– ойстроки и j –ого столбца, равен 1, если между элементами ai и аj имеет место отношение R,или 0, если оно отсутствует:
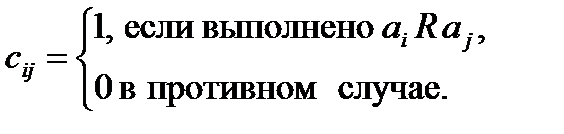
Если 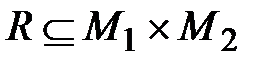 ,где M 1= { а 1, а 2,..., ап }, M 2= { b 1, b 2,..., bm }, то матрица получается прямоугольной с n строками и m столбцами.
,где M 1= { а 1, а 2,..., ап }, M 2= { b 1, b 2,..., bm }, то матрица получается прямоугольной с n строками и m столбцами.
бинарному отношению 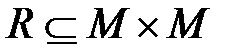 ,где M = { а 1, а 2,..., ап },соответствует ориентированный граф (орграф), вершины которого взаимно однозначно соответствуют элементам множества М,а дуги соответствуют отношениям между элементами множества М. Например, дуга, соединяющая пару элементов аi и аj внаправлении от аi к аj,показываетналичие отношения аiRаj.
,где M = { а 1, а 2,..., ап },соответствует ориентированный граф (орграф), вершины которого взаимно однозначно соответствуют элементам множества М,а дуги соответствуют отношениям между элементами множества М. Например, дуга, соединяющая пару элементов аi и аj внаправлении от аi к аj,показываетналичие отношения аiRаj.
Если 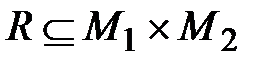 , где M 1= { а 1, а 2,..., ап }, M 2= { b 1, b 2,..., bm }, то граф получается двудольный (см. [16]): одна доля – множество вершин M 1, другая доля – множество вершин M 2, а дуги соответствуют отношениям аiRbj.
, где M 1= { а 1, а 2,..., ап }, M 2= { b 1, b 2,..., bm }, то граф получается двудольный (см. [16]): одна доля – множество вершин M 1, другая доля – множество вершин M 2, а дуги соответствуют отношениям аiRbj.
Введем следующие понятия:
Пустое отношение – отношение, которое не выполняется ни для одной пары элементов множества М. Обозначается это отношение символом  .
.
Матрица этого отношения содержит только 0, а граф состоит только из вершин (нуль граф).
Полное отношение – отношение, которое выполняется для любой пары элементов множества М. Обозначается оно U = 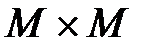 .
.
Матрица этого отношения содержит только 1. В графе этого отношения каждая вершина соединена дугой с каждой вершиной, включая ее самою (полный граф).
Диагональное отношение E (оно же тождественное отношение, оно же отношение равенства) – отношение aEb, которое выполняется только, если a и b это один и тот же элемент.
В матрице этого отношения элементы, расположенные на главной диагонали, равны 1, а остальные элементы равны 0. В графе этого отношения, кроме петель при каждой вершине, других дуг нет.
Так как отношения задаются подмножествами 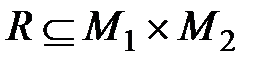 (или
(или 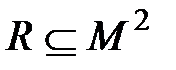 ,если М 1= М 2= М), то для них определимы те же операции, что и над множествами. Разберём эти операции более подробно.
,если М 1= М 2= М), то для них определимы те же операции, что и над множествами. Разберём эти операции более подробно.
Объединение 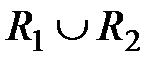 :
:
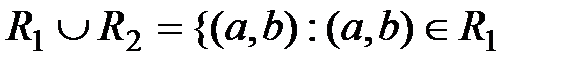 или
или 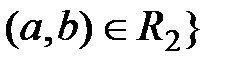 .
.
Отношение 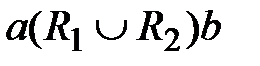 выполнено, если выполнено хотя бы одно из отношений
выполнено, если выполнено хотя бы одно из отношений 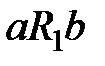 и
и 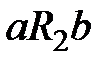 .
.
Определим объединение R 1 и R 2
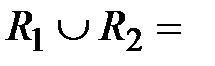 {(1,2), (1,4), (2,1), (2,3), (2,4), (3,4), (4,1), (4,3), (4,4)};
{(1,2), (1,4), (2,1), (2,3), (2,4), (3,4), (4,1), (4,3), (4,4)};
Пересечение 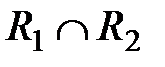 :
:
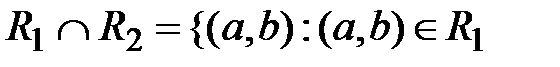 и
и 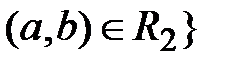 .
.
Отношение 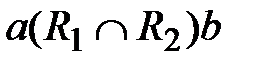 выполнено, если одновременно выполнены отношения
выполнено, если одновременно выполнены отношения 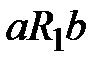 и
и 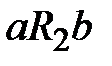 .
.
Для отношений примера 1 находим
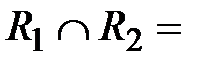 {(2,3), (2,4), (4,4)};
{(2,3), (2,4), (4,4)};
Дополнение 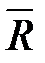 : Дополнение множества R до полного множества U – это множество таких пар, что
: Дополнение множества R до полного множества U – это множество таких пар, что 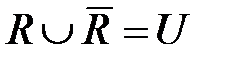 и
и 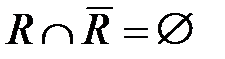 , или множество пар U без множества пар R:
, или множество пар U без множества пар R:
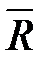 =U \ R,где U = M 1 х М 2 (или U = M 2).
=U \ R,где U = M 1 х М 2 (или U = M 2).
В нашем случае
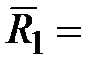 {(1,1), (1,3), (1,4), (2,1), (2,2), (3,1), (3,2), (3,3), (4,2), (4,3)};
{(1,1), (1,3), (1,4), (2,1), (2,2), (3,1), (3,2), (3,3), (4,2), (4,3)};
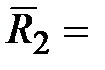 {(1,1), (1,2), (1,3), (1,4), (2,2), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2)}.
{(1,1), (1,2), (1,3), (1,4), (2,2), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2)}.
Разность R 1\ R 2:
R 1\ R 2= 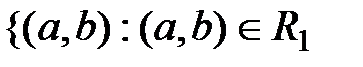 и
и 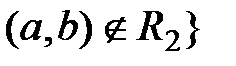 ,
,
т.е. множество пар R 1 без множества пар R 2.
Для отношений примера 1 получаем
R 1\ R 2 = {(1,2), (1,4), (3,4), (4,1)}.
Симметрическая разность
R 1  R 2 =
R 2 = 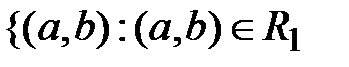 или
или 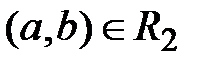 , но
, но 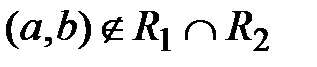 }.
}.
Это множество пар, принадлежащих или R 1 или R 2, но не принадлежащих R 1 и R 2 одновременно.
В нашем случае R 1  R 2 = {(1,2), (1,4), (2,1), (3,4), (4,1), (4,3)}.
R 2 = {(1,2), (1,4), (2,1), (3,4), (4,1), (4,3)}.
Кроме этих операций, заимствованных у множеств, над отношениями определяют такие операции:
Обратное отношение R –1:
R –1 =  .
.
Отношение bR –1 a выполняется тогда и только тогда, когда выполняется aRb.
Составное отношение (композиция, произведение) R 1○ R 2 (применяют и такое обозначение R 1 R 2).
Пусть заданы множества М 1, М 2, М 3и отношения 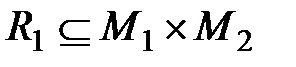 и
и 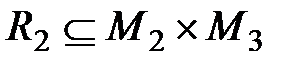 . Составное отношение действует из М 1в М 2посредством R 1, а затем из М 2в М 3посредством R 2,т.е.
. Составное отношение действует из М 1в М 2посредством R 1, а затем из М 2в М 3посредством R 2,т.е. 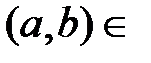 R l○ R 2,если существует такое с
R l○ R 2,если существует такое с 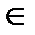 М 2, что (а, с)
М 2, что (а, с) 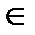 R 1и (с, b)
R 1и (с, b) 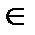 R 2. На рис. 6.4 показаны множества М 1, М 2, М 3, в них – области определений D (R 1), D (R 2) и области значений Q (R 1)и Q (R 2), заштрихованные в разных направлениях для R 1и R 2.Сегменты с двойной штриховкой на М 1, М 2, М 3представляют собой D (R 1○ R 2),
R 2. На рис. 6.4 показаны множества М 1, М 2, М 3, в них – области определений D (R 1), D (R 2) и области значений Q (R 1)и Q (R 2), заштрихованные в разных направлениях для R 1и R 2.Сегменты с двойной штриховкой на М 1, М 2, М 3представляют собой D (R 1○ R 2), 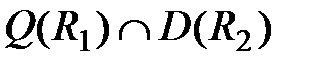 и Q (R 1○ R 2) соответственно.
и Q (R 1○ R 2) соответственно.
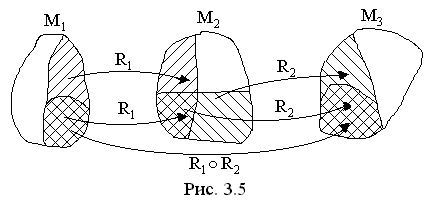
Рисунок 6.4 – Пример, поясняющий формирование
составного отношения
В частности, если отношение R определено на множестве М, R 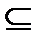 М 2, то составное отношение R ○ R= {(a, b):(a, c),(c, b)
М 2, то составное отношение R ○ R= {(a, b):(a, c),(c, b) 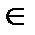 R }.
R }.
Например, если R – "быть сыном", то R ○ R – "быть внуком".
Прямое транзитивное замыкание R° состоит из таких и только таких пар элементов а, b из М,т.е. (a, b) 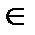 R°,длякоторых в M существует цепочка из (k+ 2)элементов М, k
R°,длякоторых в M существует цепочка из (k+ 2)элементов М, k 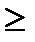 0: а, с 1, с 2,..., сk, b,между соседними элементами которой выполняется отношение R: aRc 1, c 1 Rc 2,..., ckRb,т.е. R° = {(a, b): (a, c 1),(c 1, c 2),...,(сk, b)
0: а, с 1, с 2,..., сk, b,между соседними элементами которой выполняется отношение R: aRc 1, c 1 Rc 2,..., ckRb,т.е. R° = {(a, b): (a, c 1),(c 1, c 2),...,(сk, b) 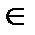 R }
R }
Это правило справедливо, если цепочка состоит и из двух элементов. Следовательно, если выполнено aRb, то выполнено и aR°b, поэтому можно записать 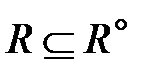 .
.
Если цепочка состоит из трех элементов, то можно записать aRс и сRb или aRRb, если цепочка состоит из четырех элементов, то aRRRb. Продолжая, можно заключить, что aR°b выполняется, если выполнено хотя бы одно отношение вида aRR… Rb. Этот факт можно записать формально в виде объединения степеней отношения R:
R° = 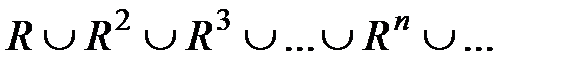
Например, для отношения R – "быть сыном" составное отношение (композиция) R ○ R = R 2 – "быть внуком", R ○ R ○ R = R 3 – "быть правнуком" и т.д. Тогда объединение всех этих отношений есть транзитивное замыкание R° – "быть прямым потомком".
Степени отношения R определяются так же, как и R ○ R = R 2 с учетом того, что Rn = Rn –1○ R.
Аналогично может быть определено обратное транзитивное замыкание:
R–° = {(d, a): (d, ek),(ek -1, ek- 2),...,(e 1, a) 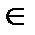 R -1}
R -1}
R–° = 
Например, для отношения R –1 – "быть сыном" составное отношение (композиция) R –1○ R –1= R– 2 – "быть отцом", R –1○ R –1○ R –1= R– 3 – "быть дедушкой" и т.д. Тогда объединение всех этих отношений есть обратное транзитивное замыкание R–° – "быть прямым предком (по мужской линии)".
Рефлексивное замыкание R*. Пусть тождественное отношение Е= {(а, а): а 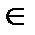 М }. Тогда R* = R°
М }. Тогда R* = R°  E.
E.
Это прямое рефлексивное замыкание. Если вместо прямого транзитивного замыкания R ° использовать обратное транзитивное замыкание R –°, то получим обратное рефлексивное замыкание R –*.
Если R транзитивно и рефлексивно, то R* = R и R–* = R –1.
Редукция Rr. Редукция применяется для отношений порядков. По смыслу эта операция обратна транзитивному замыканию. Редукцией отношения R называется отношение Rr, определяемое условием Rr = R \ R 2.
Это означает, что отношение aRrb выполняется в тех и только тех случаях, когда выполнено само отношение aRb, но не существует промежуточного элемента с такого, что aRс и сRb. Отношение aRrb означает непосредственную связь элемента a с элементом b.
 2015-03-22
2015-03-22 2123
2123