Отображения, преобразования и перестановки

Отображением множества А в множество В называется всюду определенное соответствие g: А→В,т.е. соответствие, у которого Пр₁ G = A.

Отображением А на В называется всюду определенное и при этом сюръективное соответствие g: А→В, т.е. соответствие, у которого Пр₁ G = A и Пр₂ G = B.

отображение множества A в B или A на B обозначают так .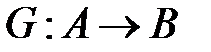

Отображение типа А → А называют преобразованием множества А.

Функция типа А→А,являющаяся отображением А на А,называется перестановкой на А.

Отображение может быть и неоднозначным. Тогда совокупность элементов b для одного a обозначается как Ga 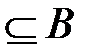. Множество Ga – этообраз элемента a в множестве B. Элемент a называется прообразом множества Ga.

Пусть имеется отображение G: А→В, где для любого a 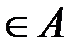образом является Ga 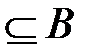, и пусть имеется множество A ₁ 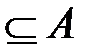. Совокупность всех 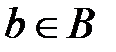, являющихся образами всех a 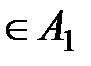, называется образом множества A ₁ и обозначается GA ₁ = .

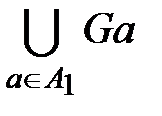Если A ₁ и A ₂ подмножества A, то образ объединения этих подмножеств равен объединению их образов в любом однозначном или неоднозначном отображении .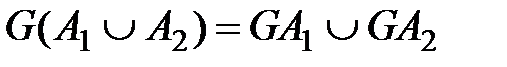

Действительно можно показать, что:

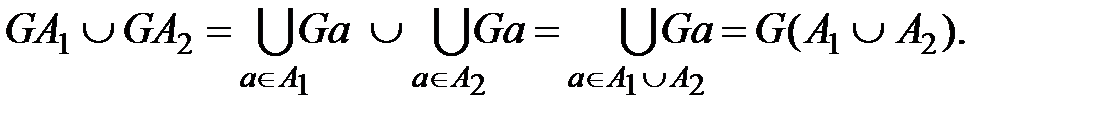
Однако соотношение будет 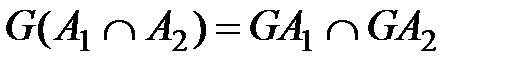, т.е. образ пересечения подмножеств равен пересечению их образов. справедливо только при однозначном отображении.

Пусть ,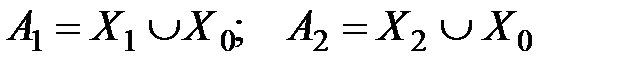

где 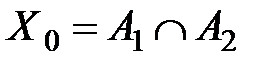– область неоднозначности.

Покажем, что

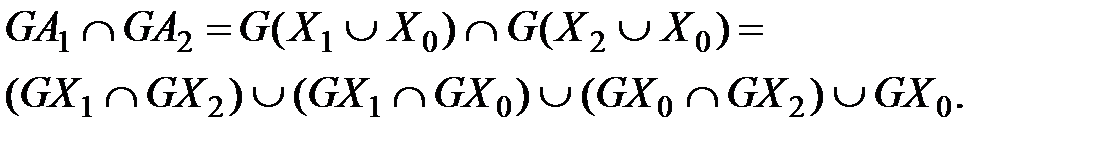
Если 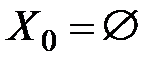(область неоднозначности пуста), то

.

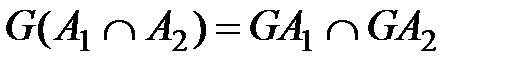Довольно часто рассматриваются отображения на одном множестве 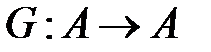, которые представляются парой (A, G), где G = A x A = A ².

Пусть G и D отображения A в A.

Композиция этих отображений будет G (D). Если D = G, то G (G) = G ², G ²(G) = G ³ и т.д.

Если принять G ⁰ = a, то это правило можно распространить и на отрицательные степени G ⁰ = G (G ^–1) = G G ^–1 = a.

Это означает, что G ^–1 является обратным отображением.

Продолжая, находим G ^–1(G ^–1) = G ^–2 и т.д.

Для отображений множеств определены прямое и обратное транзитивные замыкания – многократное отображение G или G ^–1 множества A самого на себя.

Прямое транзитивное замыкание определяется по выражению

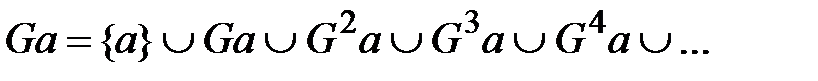для всех .

Обратное транзитивное замыкание определяется по выражению

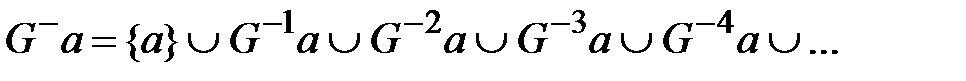для всех .