Функция, функционал, оператор

Функцией f называется однозначное соответствие, т.е. такое соответствие, при котором для пар (a ₁, b ₁) 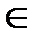f и (a ₂, b ₂) 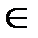f из a ₂ = a ₁ следует b ₂ = b ₁.

Если функция f устанавливает соответствие между множествами А и В,то говорят, что функция имеет тип А→В (обозначается f: А→В).

Каждому элементу а из области определения функция f ставит в соответствие элемент b из области значений. Это обозначается f (а) = b.

Элемент а – аргумент функции, элемент b — значение функции на а.

Функции f и g равны, если верны оба условия:

1) их области определения – одно и то же множество А,

2) для любого а A f (a) = g (a).

Функция типа 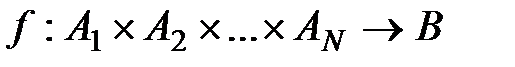называется п–местной. В этом случае принято считать, что функция имеет п аргументов:

f (a ₁,..., а_п) = b,где (a ₁,..., а_п) – кортеж, а ₁ А ₁,..., а_п А_п, b В.

Поскольку функция – это соответствие, то для нее справедливы понятия обратной функции и композиции функций, но с некоторыми уточнениями.

Если соответствие, обратное к функции f: А→В,является функциональным (однозначным), то оно называется функцией, обратной к f (обозначается ).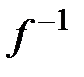

Таким образом, для функции f: А→В обратная функция существует тогда и только тогда, когда f является взаимно однозначным соответствием между своими областями определения и значений, т.е. когда функция инъекция.

Пусть даны функции f: А → В и g: В → С. Функция h: A→C называется композицией функций f и g (обозначается f ○ g или просто fg), если имеет место равенство h (x) = g (f (x)), где х А. В этом случае говорят также, что функция h получена подстановкой f в g.

Для многоместных функций f: А^т → В, и g: Вⁿ → С

возможны различные варианты подстановки f в g, дающие функции различных типов. Например, при т = 3 и п = 4 функция может иметь вид:

h = g (х ₁, f (y _l, y ₂, y ₃), x ₃, x ₄)

В данном случае функция имеет шесть аргументов и следующий тип:

B х A ³ х В ² → С.

Функция, полученная из функций f ₁,..., f_n некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией f ₁,..., f_n. Выражение, описывающее эту суперпозицию и содержащее функциональные знаки и символы аргументов и скобки, называется формулой.

Формально одноместную функцию можно записать как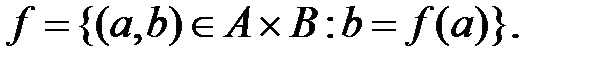

Здесь f – обозначает множество пар (a, b), f (a) – обозначает b, соответствующее данному a.

Такое определение функции позволяет установить формы задания функций:

1) перечислением пар a, b;

2) формулой b = f (a);

3) графиком в виде точек на плоскости с координатами a и b;

4) рекурсивной вычислительной процедурой.

Например, функция f (x) = 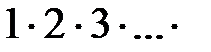(х – 1) х = х!описывается рекурсивной вычислительной процедурой:

1) f (0) = 1;

2) f (x + 1) = f (x)(х + 1).

Вот некоторые, наиболее употребляемые, способы представления функций одного аргумента (унарных функций)

Функции могут представляться перечнем всех значений аргумента а и соответствующих им значений функции b, a, b 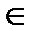M,представленных строкой:

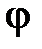= (a ₁ → b ₁, а ₂ → b ₂, ..., а_п → b_п),

а чаще парой строк:

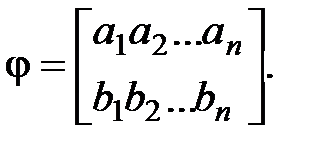
Списком всех пар "аргумент–значение" (a, b) 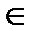φ, a, b 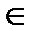М, дл я всех возможных значений аргументов:

φ = {(a ₁, b ₁), (а ₂, b ₂),..., (а_n, b_n)}.

Число таких пар |пр₁ φ| = т 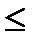| M |.

Формулой φ(а) = b,например,

lga = b (явное префиксное задание), а ² + b ² – 1 = 0 (неявное задание).

Для функций двух переменных (бинарных функций) φ: М х М → М на конечном множестве М = { a ₁, a ₂,..., а_п } наиболее часто применяют следующие способы задания.

Таблицей Кэли — таблица имеет число строк, равное числу значений аргумента a, и число столбцов, равное числу значений аргумента b. На пересечении строки, соответствующей аргументу а,и столбца, соответствующего аргументу b,записывается результат с выполненияфункцииφ над а и b.

В табл. 4.1 приведена таблица Кэли для функции, называемой "сложением по модулю 5" на множестве М= {0, 1, 2, 3, 4} и обозначаемой "+mod 5", или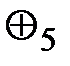

(+ mod 5)

Таблица 4.1 Таблица Кэли функции “Сложение по модулю 5”

Результат с выполнения операции 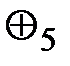равен остатку от деления суммы аргументов (а + b)на5.

Так же функции могут описываться списком всех троек (а, b, с),где а, b – соответственно первый и второй аргументы из М, с – результат выполнения функции φ над а и b, a, b, c 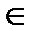M. Для всюду определенной функции число всех троек в списке | М х M | = п ².

Например, для функции сложения по модулю 3:

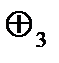= {(0,0,0), (0,1,1), (0,2,2), (1,0,1), (1,1,2), (1,2,0), (2,0,2), (2,1,0), (2,2,1)}.

Формулой φ(а, b) = с – так называемое префиксное представление, например, (а + b)mod 3 = c; иное – инфиксное представление формулой а φ b = с,например, а 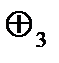b = с,где 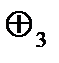– операция сложения по модулю 3.

Вот еще пример: 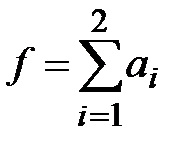и f = a ₁ + a ₂.

Если для функции n аргументов предварительно зафиксировать список (последовательность) кортежей аргументов (a ₁, a ₂,..., а_п),то для задания функции φ достаточно указать вектор значений (b ₁, b ₂,..., b_n). При этом φ(a ₁, a ₂,..., а_п) _i = b_i,т.е. результат выполнения функции φ для i –ого кортежа аргументов равен i –ойкомпоненте вектора значений. Такой способ задания функций применяется в булевой алгебре.

Рассматривая функцию стоит отдельно поговорить об о перации. Э то такая функция, у которой значения аргументов и ее собственные значения принадлежат одному и тому же множеству.

Поскольку операции это функции, то для их задания применимы все способы задания функций.

Операции обладают следующими свойствами:

Операция * идемпотентна, если x * x = x для любого x М.

Операция * коммутативна, если x * y = y * x для любых x, y М.

Операция * некоммутативна, если x * y = y * x для любых x, y М.

Операция * ассоциативна, если x * (y * z) = (x * y) * z для любых x, y, z М.

Операция * дистрибутивна относительно операции _°, если

x _° (y * z) = (x _° y) * (x _° z) для любых x, y, z М.

Операции * и _° называют взаимно обратными, если x * y = z тогда и только тогда, когда z _° y = x для любых x, y, z М.

Про операцию * говорят, что она имеет нейтральный элемент, если во множестве М существует элемент (обозначим его e), такой что x * e = x для любого x М.

Если рассматриваемая операция обозначается знаком +, то нейтральный элемент обычно называют нулём, если знаком (умножить), то – единицей.

Важное понятие ф ункционал, устанавливает связь между множеством функций и множеством чисел. Пример – определенный интеграл

,

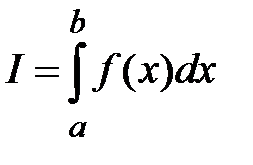где f (x) – функция, a и b – пределы интегрирования, I – число.

Другой пример функционала – наибольшее значение функции f (x) на интервале [ a, b ].

Оператор определяет еще одну разновидность связи между функциями. Еще, как пример, можно привести оператор дифференцирования Dx = df (x)/ dx. Например, пусть f (x) = sin (x), тогда df (x)/ dx = cos (x).