Наиболее часто в теории множеств возникает необходимость доказательства равенства соотношений типа Х = Y.
Доказательство можно проводить путем рассуждений с применением законов и тождеств алгебры множеств, построением диаграмм Эйлера–Венна или на примерах конкретных множеств. Ниже, в примерах, доказательства соотношений типа X = Y, где Х и Y – множества, основаны на использовании
Докажем справедливость соотношения:
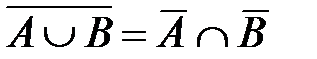 .
.
Предположим, что произвольный элемент 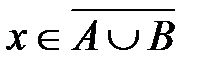 , т.е. что
, т.е. что 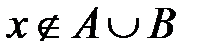 . Это значит, что
. Это значит, что 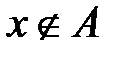 и
и 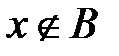 , значит
, значит 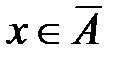 и
и 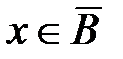 .
.
Следовательно, 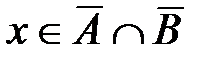 .
.
Пусть теперь некоторый элемент 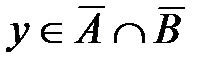 , т.е.
, т.е. 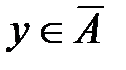 и
и 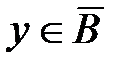 . Это значит, что
. Это значит, что 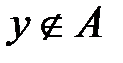 и
и 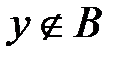 , т.е.
, т.е. 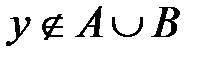 .
.
Следовательно, 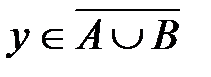 .
.
Таким образом, доказано, что 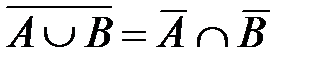 .
.
 2015-03-22
2015-03-22 781
781








