Если все каналы обслуживания заняты, заявка, поступившая в систему, становится в очередь. Если время пребывания в очереди и число мест в очереди неограниченно, то такая система называется чистой системой с ожиданием. Предельный стационарный режим при 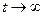 существует, если
существует, если 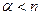 , то есть “мощность” системы достаточна для обслуживания данного потока заявок. В случае
, то есть “мощность” системы достаточна для обслуживания данного потока заявок. В случае 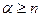 очередь будет неограниченно расти и предельного стационарного режима не существует. Кроме числовых характеристик, аналогичных характеристикам СМО с отказом, система с ожиданием обладает специфическими характеристиками, связанными с наличием очереди: средняя длина очереди, вероятность наличия очереди, среднее время пребывания заявки в очереди и некоторыми другими.
очередь будет неограниченно расти и предельного стационарного режима не существует. Кроме числовых характеристик, аналогичных характеристикам СМО с отказом, система с ожиданием обладает специфическими характеристиками, связанными с наличием очереди: средняя длина очереди, вероятность наличия очереди, среднее время пребывания заявки в очереди и некоторыми другими.
Предельные вероятности состояний системы (при условии существования стационарного режима работы) определяются по формулам:
1) В случае отсутствия очереди
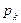 =
= 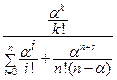 , где
, где 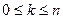 .
.
2) В случае наличия очереди
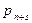 =
= 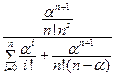 , где s – длина очереди, s =1,2,3,….
, где s – длина очереди, s =1,2,3,….
Среднее число заявок, находящихся в очереди, определяется по формуле:
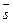 =
= 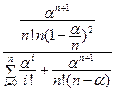 .
.
Для СМО с ожиданием 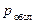 =1. Среднее число занятых каналов
=1. Среднее число занятых каналов 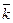 =
= 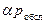 =
= 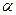 . Система имеет бесконечное число состояний,
. Система имеет бесконечное число состояний, 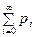 =1. Среднее время ожидания заявки в очереди
=1. Среднее время ожидания заявки в очереди 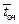 =
= 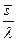 .
.
Задача. Рассматривается работа таможенного пропускного пункта автомобилей на границе. Пункт имеет 3 поста. В среднем каждые 3 минуты к границе подъезжает автомобиль. За 1 час каждый пост, в среднем, может проверить и пропустить 10 автомобилей. Число мест в очереди и время пребывания в очереди практически не ограничено. Определить, существует ли стационарный режим работы пропускного пункта. Если да, то найти:
1) вероятности состояний системы
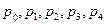 ,
, 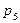 ;
;
2) вероятность наличия очереди 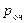 ;
;
3) среднюю длину очереди 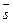 ;
;
4) среднее число занятых каналов (постов) 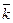 ;
;
5) вероятность занятости канала (поста) 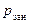 ;
;
6) среднее время ожидания машины в очереди 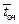 ;
;
7) среднее время простоя поста.
Решение. Из условия задачи число каналов 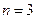 ;
; 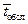 =1/20 часа;
=1/20 часа; 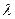 = 20 машин в час;
= 20 машин в час; 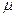 = 10;
= 10; 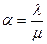 =2. Найдем
=2. Найдем
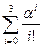 =
= 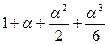 =1+2+2+4/3=19/3;
=1+2+2+4/3=19/3;
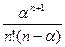 =
= 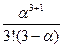 =16/6=8/3.
=16/6=8/3.
В итоге знаменатель дробей в формулах вероятностей состояний равен 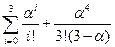 =19/3+8/3=9.
=19/3+8/3=9.
1) Найдем вероятности 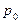 =1/9;
=1/9;  =2/9;
=2/9; 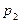 =2/9;
=2/9; 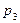 =4/27. Вероятность
=4/27. Вероятность 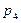 соответствует случаю занятости всех постов и одной машине в очереди, то есть s =1. Для вычисления
соответствует случаю занятости всех постов и одной машине в очереди, то есть s =1. Для вычисления 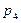 используем формулу
используем формулу 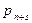 =
= 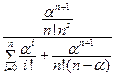 .
.
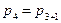 =
= 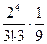 =
= 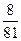 ;
;
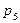 =
= 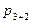 =
= 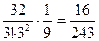 (случай s =2).
(случай s =2).
2) Вероятность наличия очереди определяем так:
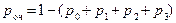 =1-(1/9+2/9+2/9+4/27)=8/27.
=1-(1/9+2/9+2/9+4/27)=8/27.
3) Определим среднюю длину очереди
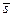 =
= 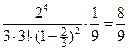 .
.
4) Так как 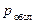 =1, то
=1, то 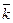 =
= 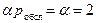 .
.
5) Найдем вероятность занятости канала 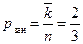 .
.
6) Среднее время простоя поста равно
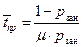 = 1/20=0.05 (ч.)
= 1/20=0.05 (ч.)
Из полученных результатов видно, что пропускной пункт хорошо выполняет свои функции, очередь невелика, и есть определенный резерв при увеличении потока автомобилей.
Задача 8.4. Рассматривается работа автозаправочной станции (АЗС), на которой имеется 4 заправочные колонки. Заправка одной машины длится в среднем 6 минут. В среднем, каждые 3 минуты на АЗС прибывает машина, нуждающаяся в заправке. Число мест в очереди практически не ограничено. Все машины, вставшие в очередь, терпеливо дожидаются заправки, так как других АЗС поблизости нет. Определить, существует ли стационарный режим работы СМО. Если нет, то уменьшите среднее время обслуживания одной машины и повторите расчеты. Если стационарный режим существует, определите:
1) вероятности pi (i = 0, 1, 2, 3, 4);
2) вероятности наличия очереди p оч;
3) среднюю длину очереди 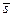 ;
;
4) среднее число занятых колонок 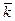 ;
;
5) вероятности занятости каждой колонки p зан;
6) среднее время ожидания машины в очереди 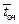 ;
;
7) среднее время простоя колонки 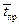 .
.
Решение. Из условия задачи число каналов 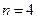 ;
; 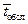 =1/20 часа;
=1/20 часа; 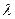 =20 машин в час;
=20 машин в час; 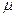 =10;
=10; 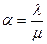 =2. Найдем
=2. Найдем
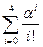 =
= 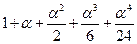 =1+2+2+4/3+2/3=21/3;
=1+2+2+4/3+2/3=21/3;
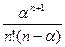 =
= 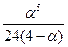 =4/6=2/3.
=4/6=2/3.
В итоге знаменатель дробей в формулах вероятностей состояний равен 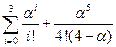 =21/3+2/3=23/3.
=21/3+2/3=23/3.
1) Найдем вероятности загруженности 0, 1, 2, 3 и 4 каналов.
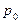 =
= 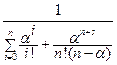 =
= 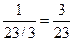 ;
;
 =
= 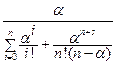 =
= 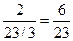 ;
;
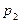 =
= 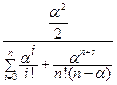 =
= 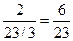 ;
;
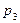 =
= 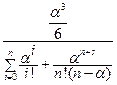 =
= 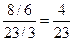 ;
;
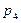 =
= 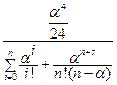 =
= 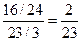 .
.
Вероятность 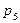 соответствует случаю занятости всех постов и одной машине в очереди, то есть s =1, вероятность
соответствует случаю занятости всех постов и одной машине в очереди, то есть s =1, вероятность 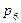 - случаю
- случаю 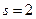 машинам в очереди, и т.д. Для вычисления
машинам в очереди, и т.д. Для вычисления 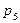 ,
, 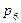 , ¼, используем формулу
, ¼, используем формулу
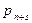 =
= 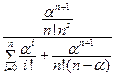 .
.
Получаем:
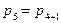 =
= 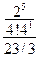 =
= 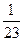 ;
;
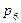 =
= 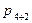 =
= 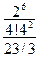 =
= 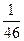 ;
;
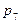 =
= 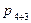 =
= 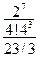 =
= 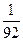 ¼
¼
2) Вероятность наличия очереди определяем так:
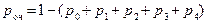 = 1 - (3/23 + 6/23 + 6/23 +
= 1 - (3/23 + 6/23 + 6/23 +
+4/23 + 2/23) = 2/23.
3) Определим среднюю длину очереди
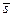 =
= 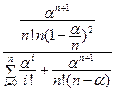 =
= 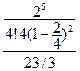 = 4/23.
= 4/23.
4) Так как 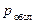 =1, то
=1, то 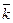 =
= 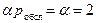 .
.
5) Найдем вероятность занятости канала 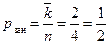 .
.
6) Среднее время простоя поста равно
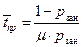 =
= 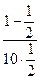 =0.1 (ч.)
=0.1 (ч.)
 2015-03-22
2015-03-22 4175
4175








