Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема п.
Выборочной средней 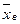 называют среднее арифметическое значение признака выборочной совокупности:
называют среднее арифметическое значение признака выборочной совокупности:
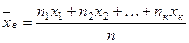 , или
, или 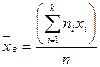 .
.
хi – варианта выборки, пi – частота варианты хi, 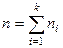 - объем выборки.
- объем выборки.
Рассмотрим некоторую совокупность, значений количественного признака Х объема п:
| Значение признака | х1 | х2 | … | хк |
| Частота | п1 | n2 | … | пк |
причем 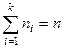 .
.
Отклонением называют разность 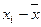 между значением признака и общей средней.
между значением признака и общей средней.
Теорема. Сумма произведений отклонений на соответствующие частоты равна нулю
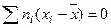 .
.
 2015-03-22
2015-03-22 1715
1715
