Производная по направлению некоторого вектора 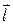 характеризует скорость изменения функции
характеризует скорость изменения функции 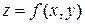 в точке
в точке 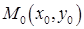 вдоль этого вектора.
вдоль этого вектора.
Если функция 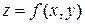 имеет в точке
имеет в точке 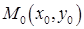 непрерывные частные производные, то в этой точке существует производная
непрерывные частные производные, то в этой точке существует производная 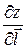 по направлению
по направлению 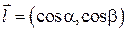 , где
, где 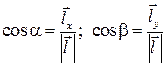 ;
; 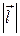 – длина вектора
– длина вектора 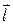 , причем
, причем
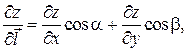
где значения частных производных 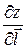 ,
, 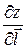 вычисляются в точке
вычисляются в точке 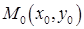 .
.
Вектор с координатами 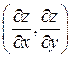 , характеризующий направление максимального роста функции в точке
, характеризующий направление максимального роста функции в точке 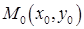 , называют градиентом функции в этой точке и обозначают
, называют градиентом функции в этой точке и обозначают 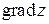 .
.
Производная по направлению и градиент связаны соотношением
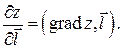
Для функции трех переменных 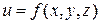 направление
направление 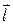 задается вектором
задается вектором 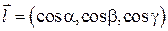 , где
, где 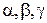 – углы между вектором
– углы между вектором 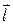 и положительными направлениями осей
и положительными направлениями осей 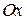 ,
, 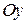 ,
, 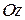 , а
, а 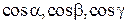 называют направляющими косинусами вектора
называют направляющими косинусами вектора 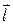 .
.
Тогда
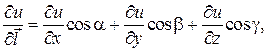
где 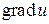 есть вектор с координатами
есть вектор с координатами 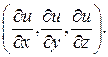
Пример 5.1. Для функции 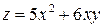 найти градиент и производную по направлению вектора
найти градиент и производную по направлению вектора 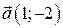 в точке
в точке 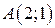 .
.
Решение. Найдем координаты вектора 
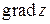 в точке
в точке 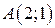 согласно определению
согласно определению 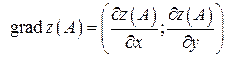 .
.
Вычислим частные производные и найдем их значения в точке 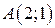 :
:
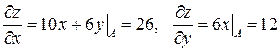 .
.
Таким образом, 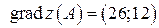 .
.
Длину вектора 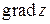 определим по формуле
определим по формуле
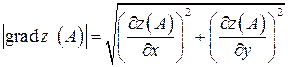 ,
,
Тогда, учитывая найденные координаты вектора, получим
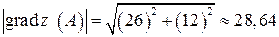 .
.
Далее найдем производную в точке 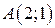 по направлению вектора
по направлению вектора 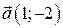 . Как известно,
. Как известно,
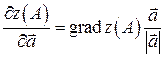 ,
,
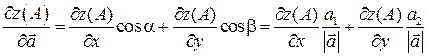 ,
,
где 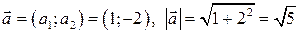 .
.
Тогда производная по направлению вектора 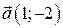 в точке
в точке 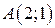 равна
равна
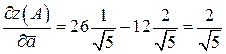 .
.
5.1. Верно ли следующее утверждение: градиентом функции 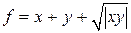 в точке
в точке 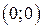 является вектор
является вектор 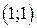 ?
?
Найти производную функции 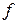 по направлению вектора
по направлению вектора 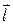 в точке
в точке 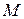 , если:
, если:
5.2. 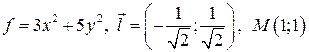 .
.
5.3. 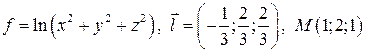 .
.
Найти производную функции 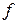 в точке
в точке  по направлению вектора
по направлению вектора 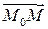 , если:
, если:
5.4. 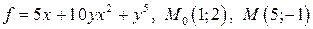 .
.
5.5. 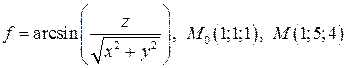 .
.
5.6. Показать, что в точке 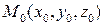 угол между градиентами функций
угол между градиентами функций
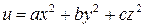
и
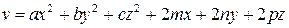 ,
,
где 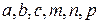 – константы, а
– константы, а 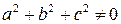 стремится к нулю, если точка
стремится к нулю, если точка  удаляется в бесконечность.
удаляется в бесконечность.
5.7. Решить уравнение 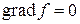 , если
, если
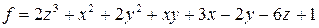 .
.
5.8. Найти наибольшее значение производной 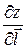 в точке
в точке 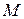 , если
, если
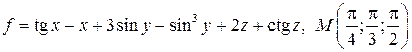 .
.
Ответы: 5.1. Неверно. 5.2. 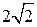 . 5.3.
. 5.3. 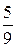 . 5.4.
. 5.4. 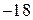 . 5.5.
. 5.5. 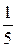 . 5.7.
. 5.7. 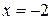 ,
, 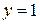 ,
, 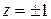 . 5.8.
. 5.8. 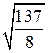 .
.
 2015-03-27
2015-03-27 2253
2253
