Теорема существования. Если:
1) функция 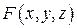 обращается в нуль в некоторой точке
обращается в нуль в некоторой точке 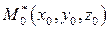 ;
;
2) 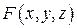 и
и 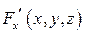 определены и непрерывны в окрестности точки
определены и непрерывны в окрестности точки 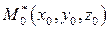 ;
;
3) 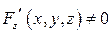 ,
,
то в некоторой достаточно малой окрестности точки 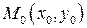 существует единственная однозначная непрерывная функция
существует единственная однозначная непрерывная функция
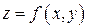 ,
,
удовлетворяющая уравнению
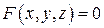
и такая, что 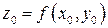 .
.
Частные производные функций, заданных неявно. Если выполнены все условия приведенной выше теоремы и, кроме того, функция 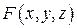 дифференцируема в окрестности точки
дифференцируема в окрестности точки 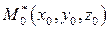 , то функция
, то функция 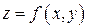 дифференцируема в окрестности точки
дифференцируема в окрестности точки 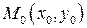 и ее производные
и ее производные 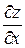 и
и 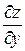 могут быть найдены из уравнений
могут быть найдены из уравнений
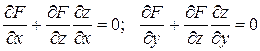 .
.
Если функция 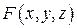 дифференцируема достаточное число раз, то последовательным дифференцированием этих уравнений вычисляются производные высших порядков от функции
дифференцируема достаточное число раз, то последовательным дифференцированием этих уравнений вычисляются производные высших порядков от функции 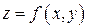 .
.
Дифференцирование неявных функций, заданных системой уравнений. Пусть функции 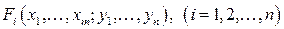 удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1) обращаются в нуль в точке 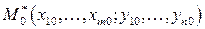 ;
;
2) дифференцируемы в окрестности точки 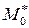 ;
;
3) функциональный определитель (якобиан) 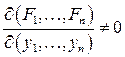 в точке
в точке 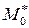 .
.
Тогда система уравнений
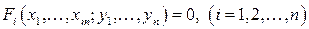
однозначно определяет в некоторой окрестности точки 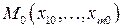 систему дифференцируемых функций
систему дифференцируемых функций
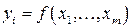 ,
, 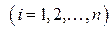 ,
,
удовлетворяющих системе уравнений 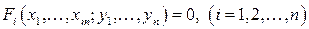 и начальным условиям
и начальным условиям
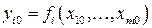 ,
, 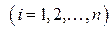 .
.
Дифференциалы этих неявных функций могут быть найдены из системы
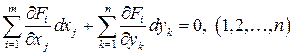 .
.
Пример 6.1. Найти в точке (1;1) частные производные функции 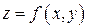 , заданной неявно уравнением
, заданной неявно уравнением
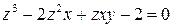 .
.
Решение. Из уравнения найдем значение функции 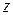 в данной точке:
в данной точке:
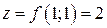 . Функция
. Функция 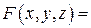
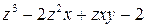 равна нулю в точке (1;1;2) и непрерывна в ее окрестности, а ее частные производные
равна нулю в точке (1;1;2) и непрерывна в ее окрестности, а ее частные производные
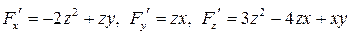
также непрерывны, 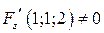 .
.
Поэтому функция 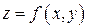 является непрерывно дифференцируемой в окрестности точки (1;1;2) и ее частные производные можно найти по формулам:
является непрерывно дифференцируемой в окрестности точки (1;1;2) и ее частные производные можно найти по формулам:
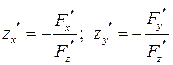 .
.
Тогда
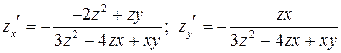 ,
,
а значение в точке (1;1;2):
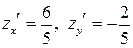 .
.
Пример 6.2. Найти производные первого и второго порядков неявных функций 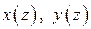 в точке
в точке 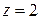 , если эти функции заданы системой уравнений
, если эти функции заданы системой уравнений
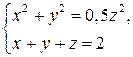 (1)
(1)
и удовлетворяют условиям 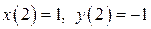 .
.
Решение. Функции
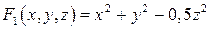 и
и 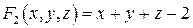
дифференцируемы в окрестности точки 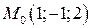 . Частные производные
. Частные производные
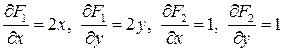
непрерывны в точке 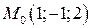 . Так как
. Так как 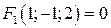 и
и 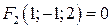 , а якобиан в точке
, а якобиан в точке 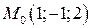 отличен от нуля, т. е.
отличен от нуля, т. е.
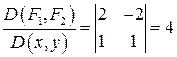 ,
,
то система уравнений (1) определяет единственную пару функций 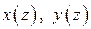 , дважды дифференцируемых в окрестности точки
, дважды дифференцируемых в окрестности точки 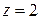 .
.
Продифференцируем систему (1) по переменной 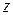 :
:
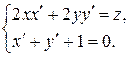 (2)
(2)
Подставив координаты точки 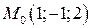 в эту систему, получим
в эту систему, получим
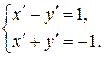
Тогда 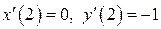 . Еще раз продифференцируем по
. Еще раз продифференцируем по 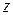 систему (2):
систему (2):
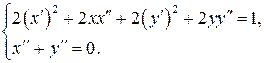
В точке 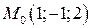 имеем
имеем
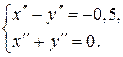
Тогда 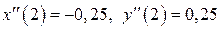 .
.
6.1. Уравнение 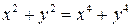 определяет
определяет 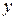 как многозначную функцию от
как многозначную функцию от 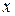 . В каких областях эта функция: 1) однозначна, 2) двузначна, 3) трехзначна, 4) четырехзначна? Определить точки ветвления этой функции и ее однозначные ветви.
. В каких областях эта функция: 1) однозначна, 2) двузначна, 3) трехзначна, 4) четырехзначна? Определить точки ветвления этой функции и ее однозначные ветви.
Найти 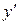 и
и 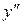 для функций, определяемых следующими уравнениями:
для функций, определяемых следующими уравнениями:
6.2. 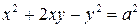 . . | 6.3. 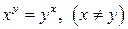 . . |
6.4. Доказать, что для кривой второго порядка
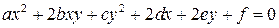
справедливо равенство
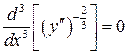 .
.
Для функции 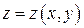 найти частные производные первого и второго порядков, если:
найти частные производные первого и второго порядков, если:
6.5. 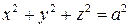 . . | 6.6. 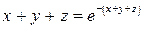 . . |
6.7. Найти 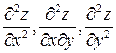 при
при 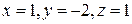 , если
, если
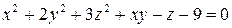 .
.
Найти 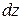 и
и 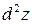 , если:
, если:
6.8. 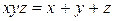 . . | 6.9. 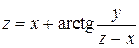 . . |
6.10. Найти 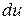 , если
, если 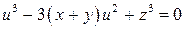 .
.
6.11. Найти 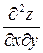 , если
, если 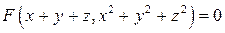 .
.
6.12. Найти 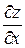 и
и 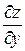 , если
, если 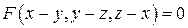 .
.
6.13. Найти 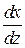 и
и 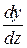 , если
, если 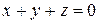 ,
, 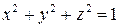 .
.
6.14. Система уравнений
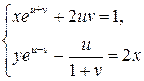
определяет дифференцируемые функции 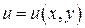 и
и 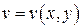 такие, что
такие, что 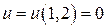 и
и 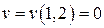 . Найти
. Найти 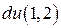 и
и 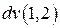 .
.
6.15. Функция 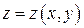 задана уравнением
задана уравнением
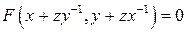 .
.
Показать, что
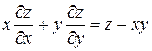 .
.
Ответы: 6.1. 1) нигде; 2) 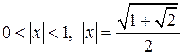 ; 3)
; 3) 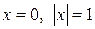 ; 4)
; 4) 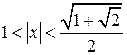 ; однозначные ветви:
; однозначные ветви: 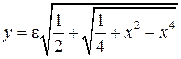 ,
,
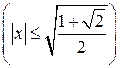 ;
; 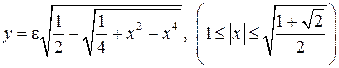 , где
, где 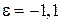 . 6.2.
. 6.2. 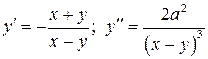 . 6.3.
. 6.3. 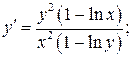
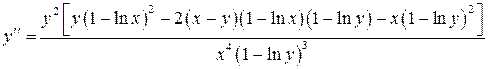 .
.
6.5. 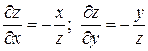 ;
; 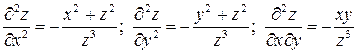 . 6.6.
. 6.6. 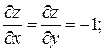
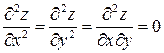 .
.
6.7. 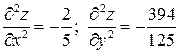 ;
; 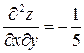 .
.
6.8. 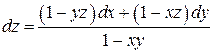 ;
;
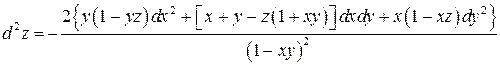 .
.
6.9. 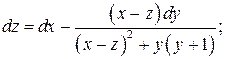
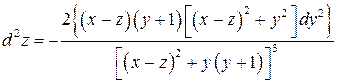 .
.
6.10. 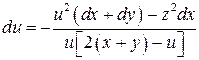 .
.
6.11. 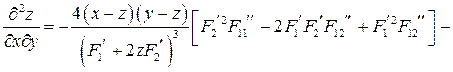
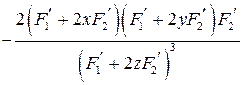 . 6.12.
. 6.12. 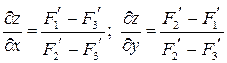 .
.
6.13. 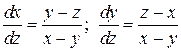 . 6.14.
. 6.14. 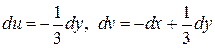 .
.
 2015-03-27
2015-03-27 5115
5115
