7.4.1. Непосредственное интегрирование
Способ непосредственного интегрирования основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме.
Пример. Найти интегралы:
1) 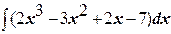 .
.
Решение. На основании свойств 3 и 4 неопределенного интеграла и таблицы интегралов имеем
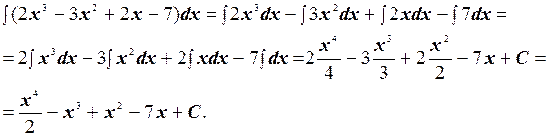
2) 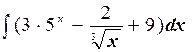 .
.
Решение. Воспользуемся свойствами 3 и 4 неопределенного интеграла:
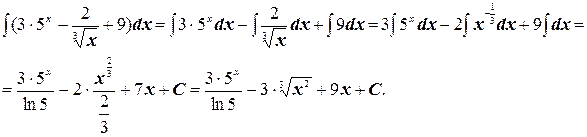
3) 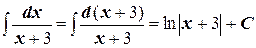 .
.
7.4.2. Метод подстановки (замена переменной)
Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных.
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:
1) 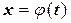 , где t – новая переменная, а φ (t) – функция, имеющая непрерывную производную. Тогда формула замены переменной
, где t – новая переменная, а φ (t) – функция, имеющая непрерывную производную. Тогда формула замены переменной
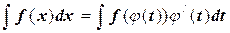 .
.
2) 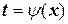 , t – новая переменная. Формула замены переменной при такой подстановке:
, t – новая переменная. Формула замены переменной при такой подстановке:
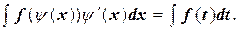
Пример. Найти интегралы, используя подходящую подстановку:
1) 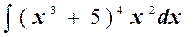 .
.
Решение. Введем подстановку t = x 3+5. Тогда dt = d (x 3+5); dt =3 x 2 dx. Отсюда x 2 dx = dt /3. Таким образом,
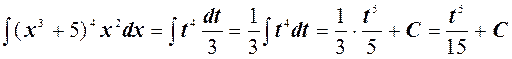 .
.
Ответ должен быть выражен через «старую» переменную х. Подставляя в результат интегрирования t = x 3+5. Окончательно получим 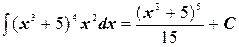 .
.
2) 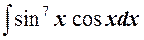 .
.
Решение.
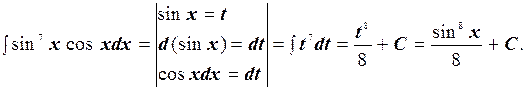
Условимся в дальнейшем все промежуточные рассуждения и выкладки заключать в вертикальные скобки (как было сделано в примере 2).
7.4.3. Интегрирование по частям
Интегрированием по частям называется нахождение интеграла по формуле
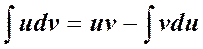 , (6.4.1)
, (6.4.1)
где u и v непрерывно дифференцируемые функции от х. С помощью формулы (6.4.1) нахождение интеграла 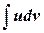 сводится к нахождению другого интеграла
сводится к нахождению другого интеграла 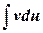 . Применение этой формулы целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
. Применение этой формулы целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом в качестве u берется функция, которая при дифференцировании упрощается, а в качестве dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Пример. При нахождении интеграла 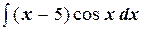 , полагая u = x –5, dv = cos xdx, найдем du = dx,
, полагая u = x –5, dv = cos xdx, найдем du = dx, 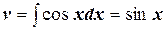 . Следовательно, применяя формулу (6.4.1), получим
. Следовательно, применяя формулу (6.4.1), получим
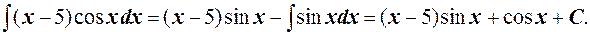
 2015-03-07
2015-03-07 512
512








