1. Определенный интеграл не зависит от обозначения переменной интегрирования, т.е.
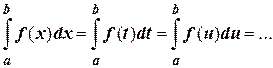
2. 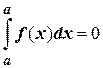
3. Определенный интеграл от суммы конечного числа непрерывных функций f 1(x), f 2(x), …, fn (x), заданных на отрезке [ a; b ], равен сумме определенных интегралов от этих функций:
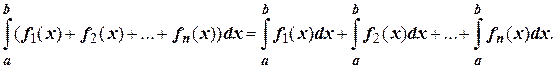
4. Постоянный множитель можно выносить за знак определенного интеграла:
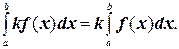
5. 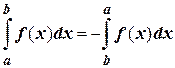
6. 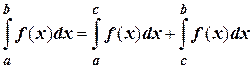 , где a < c < b.
, где a < c < b.
7. Если f (x) ³0 на отрезке [ a; b ], то 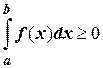 ; если f (x) £0 на отрезке [ a; b ], то
; если f (x) £0 на отрезке [ a; b ], то 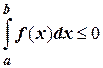 .
.
8. Если m, M – соответственно наименьшее и наибольшее значения функции f (x) на отрезке [ a; b ]: m £ f (x)£ M, то 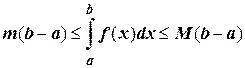 .
.
9. Если f (x) £ g (x) на отрезке [ a; b ], то 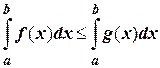 .
.
10. Определенный интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке х = с отрезка интегрирования [ a; b ] на длину этого отрезка (теорема о среднем):
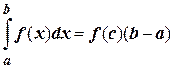 или
или 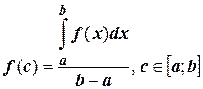 .
.
11. 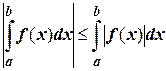 .
.
12. 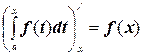 .
.
 2015-03-07
2015-03-07 430
430








