Первообразная функция и неопределенный интеграл

Пусть функция f (x) определена на некотором (конечном или бесконечном) интервале (а; b). Функция F (x) называется первообразной для функции f (x) на интервале (а; b),если в любой точке этого промежутка ее производная равна f(x), т. е.

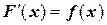для всех 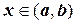или dF (x) = f (x) dx.

функция 3 x ² есть производная от x ³, т. е. 3 x ² dx есть дифференциал функции x ³:

3 x ² dx = d (x ³ ).

Тогда, по определению функция x ³ является первообразной для функции 3 x ². Кроме того, выражение 3 x ² dx есть дифференциал функции x ³+7: 3 x ² dx = d (x ³+7 ).

Следовательно, функция x ³+7 (как и функция x ³) – первообразная для функции 3 x ².

Если F (x) есть одна из первообразных для функции f (x), то всякая другая представляется выражением F (x)+ C, где C – произвольная постоянная величина.

Таким образом, любая непрерывная функция f (x) имеет бесчисленное множество первообразных.

Неопределенным интегралом от функции f (x) (или от выражения f (x) dx) называется совокупность всех ее первообразных.

Обозначение: .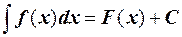

Здесь знак 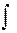называется интегралом, функция f (x) – подынтегральной функцией, f (x) dx – подынтегральным выражением, х – переменной интегрирования.

Операция нахождения неопределенного интеграла от данной функции называется интегрированием этой функции.

Интегрирование – операция, обратная операции дифференцирования (нахождения производной от функции). Всякая непрерывная на данном интервале функция имеет неопределенный интеграл.