Приведем основные свойства неопределенного интеграла или правила интегрирования. Предполагается, что все рассматриваемые неопределенные интегралы существуют.
1. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:
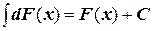 .
.
2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
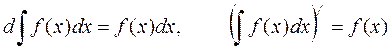
3. Неопределенный интеграл суммы функций равен сумме неопределенных интегралов этих функций:
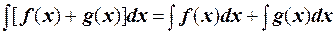 .
.
4. Постоянный множитель 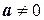 можно выносить за знак неопределенного интеграла:
можно выносить за знак неопределенного интеграла:
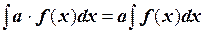 .
.
5. Если F (x) первообразная для функции f (x), то 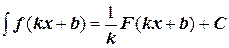 , где k и b – постоянные.
, где k и b – постоянные.
Таблица простейших интегралов
1. 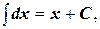
2. 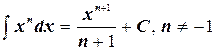
3. 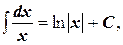
4. 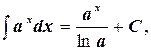
5. 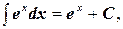
6. 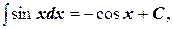
7. 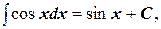
8. 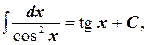
9. 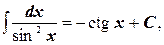
10. 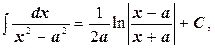
11. 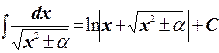
12. 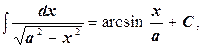
13. 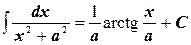 ,
,
14. 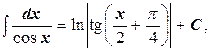
15. 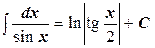 ,
,
16. 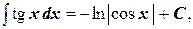
17. 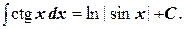
 2015-03-07
2015-03-07 333
333








