Свойства дифференциала функции

1) .

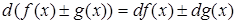2)

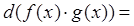
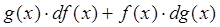
3)

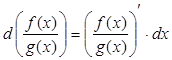
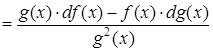
4)

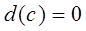
5)

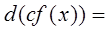
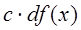
Дифференциал сложной функции. Свойство инвариантности.

Рассмотрим свойство дифференциала функции, вытекающее из правила дифференциала сложной функции.

Пусть 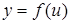и 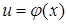– непрерывные функции своих аргументов, имеющие производные по этим аргументам 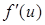и 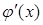. Если обозначить 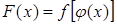, то 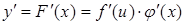. Умножая обе части уравнения на 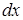, получим:

,

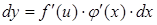но 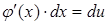, и значит,

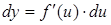
т.е. дифференциал 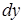имеет такой же вид, как если бы величина 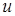была бы независимой переменной.

Дифференциал функции 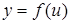сохраняет одно и то же выражение, независимо от того, является ли ее аргумент 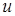независимой переменной или функцией от независимой переменной.

Это свойство называется инвариантностью (т.е. неизменностью) формы дифференциала.