Пусть в точке 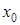 производная функции
производная функции 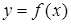 отлична от нуля:
отлична от нуля: 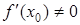 . Тогда
. Тогда
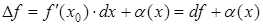 ,
,
где 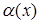 – б/м величина при
– б/м величина при 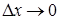 более высокого порядка, чем
более высокого порядка, чем 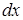 .Но при указанном условии она будет б/м величиной более высокого порядка и чем
.Но при указанном условии она будет б/м величиной более высокого порядка и чем 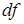 и
и 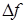 . Действительно, при
. Действительно, при 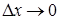 имеем:
имеем:
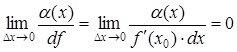 ,
,
ибо 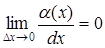 , а
, а 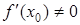 . Значит,
. Значит, 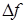 и
и 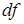 отличаются друг от друга на бесконечно малую величину более высокого порядка, чем они сами, и, следовательно, они эквивалентны:
отличаются друг от друга на бесконечно малую величину более высокого порядка, чем они сами, и, следовательно, они эквивалентны:
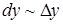 .
.
Отсюда получаем приближенную формулу вычисления:
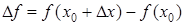 ,
, 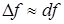 , следовательно,
, следовательно,
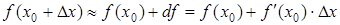
Формула называется формулой приближенного вычисления с помощью дифференциала.
Пример 1. Вычислить приближенно 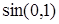 .
.
Решение. Имеем: 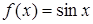 ,
, 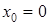 ,
, 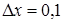 . Тогда:
. Тогда:
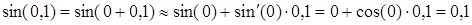 .
.
Пример 2. Вычислить приближенно 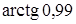 .
.
Решение. Имеем: 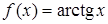 ,
, 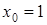 ,
, 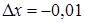 . Тогда:
. Тогда:
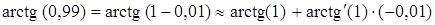 .
.
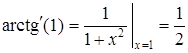 ,
, 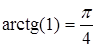 , следовательно,
, следовательно,
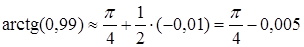 .
.
 2015-03-27
2015-03-27 260
260








