Тема 5. Дифференциал функции.

Рассмотрим функцию 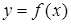 , которая определена и непрерывна в точке
, которая определена и непрерывна в точке 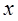 и некоторой ее окрестности и дифференцируема в точке
и некоторой ее окрестности и дифференцируема в точке 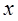 .
.
Функция дифференцируема, следовательно, существует ее производная
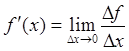 .
.
Предел можно представить как 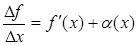 ,
,
где 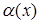 – БМВ, следовательно,
– БМВ, следовательно,
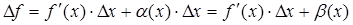 ,
,
где 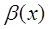 – БМВ.
– БМВ.



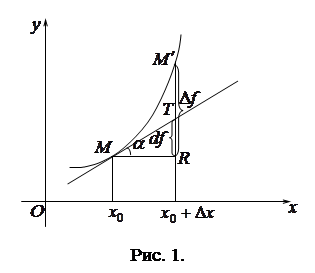
Рассмотрим геометрическую иллюстрацию дифференциала функции 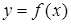 (Рис. 1). Т.к.
(Рис. 1). Т.к. 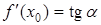 , то дифференциал
, то дифференциал 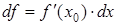 измеряет отрезок
измеряет отрезок  .
.
 Дифференциал
Дифференциал 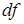 функции
функции 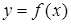 в точке
в точке 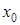 численно равен приращению ординаты касательной, построенной к графику функции в точке
численно равен приращению ординаты касательной, построенной к графику функции в точке 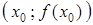 , соответствующему изменению аргумента
, соответствующему изменению аргумента 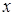 от значения
от значения 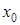 до значения
до значения 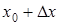 .
.
Приращение функции 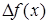 изображается приращением ординаты точки линии (отрезок
изображается приращением ординаты точки линии (отрезок 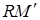 ). Поэтому разность между дифференциалом и приращением изображается отрезком
). Поэтому разность между дифференциалом и приращением изображается отрезком 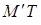 , заключенным между линией и касательной к ней; длина этого отрезка является при
, заключенным между линией и касательной к ней; длина этого отрезка является при 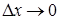 бесконечно малой величиной более высокого порядка, чем длина отрезка
бесконечно малой величиной более высокого порядка, чем длина отрезка 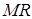
 2015-03-27
2015-03-27 278
278







