Метод непосредственного интегрирования является одним из основных методов.
Этот прием интегрирования применяется в том случае, если интеграл табличный или легко сводится к одному или нескольким табличным, путем использования свойств подынтегральной функции или следующих правил интегрирования:
1. 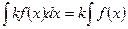 ,
,
2. 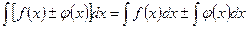 ,
,
где ¦ (х), 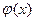 - интегрируемые функции, k=const.
- интегрируемые функции, k=const.
Пример 1. Найти 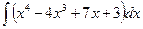 .
.
Решение. Представляя интеграл от алгебраической суммы в виде суммы интегралов слагаемых, вынося постоянные множители за знаки интегралов и применяя формулы 1, 2 таблицы основных интегралов, получим
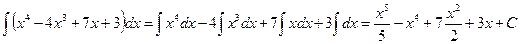 .
.
Замечание. Нет необходимости ставить произвольную постоянную после вычисления каждого интеграла, т.к. их сумма есть также произвольная постоянная, которую обозначают одной буквой и записывают в окончательный ответ.
Пример 2. Найти 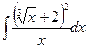 .
.
Решение. Возведём двучлен в квадрат и запишем каждое слагаемое в виде степенной функции, затем, произведя почленное деление и применив формулы 2, 3 таблицы основных интегралов, получим
 .
.
Пример 3. Найти 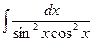 .
.
Решение. Заменив единицу в числителе выражением sin²x+cos²x и почленно разделив числитель на знаменатель, получим
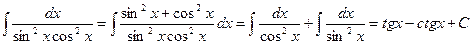 .
.
Пример 4. Найти 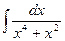 .
.
Решение. Прибавим и вычтем х² в числителе подынтегральной функции, вынесем за скобки х2 в знаменателе и почленно разделим числитель на знаменатель. Получим:
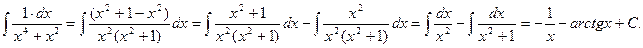 Пример 5. Найти
Пример 5. Найти 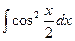 .
.
Решение. Воспользуемся формулой тригонометрии 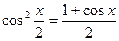 . Тогда получим
. Тогда получим
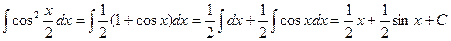 .
.
2.5.4.2.Метод подстановки
Во многих случаях удаётся введением вместо х новой переменной t, связанной с х некоторым соотношением, свести 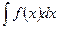 к новому интегралу, который содержится в таблице или легко находится другим методом.
к новому интегралу, который содержится в таблице или легко находится другим методом.
Этот метод получил название метода замены переменной или метода интегрирования подстановкой.
Теорема: Пусть 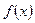 – непрерывная функция и дан интеграл
– непрерывная функция и дан интеграл 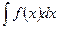 . Вместо х введём новую переменную t, связанную с х соотношением
. Вместо х введём новую переменную t, связанную с х соотношением 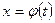 , где
, где 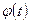 – непрерывная, строго монотонная функция, имеющая непрерывную производную
– непрерывная, строго монотонная функция, имеющая непрерывную производную 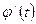 . Тогда
. Тогда 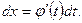
На основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
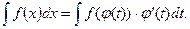
Пример 1. Найти 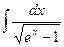 .
.
Решение. Пусть 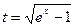 , тогда
, тогда 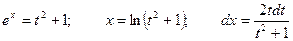 .
.
Подставляя в исходный интеграл, получим: 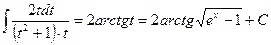 .
.
Пример 2. Найти 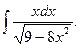
Решение. Пусть 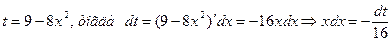
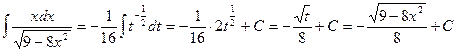
 2015-03-07
2015-03-07 7771
7771
