Метод интегрирования по частям следует из формулы дифференцирования произведения двух функций. Известно, что интеграл от произведения функций не равен произведению интегралов, здесь существует более сложная зависимость.
Если u=u(x) и v=v(x) – две дифференцируемые функции от х, то по правилу дифференцирования произведения имеем
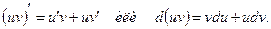
интегрируя обе части, получим:
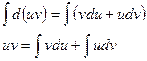
Выразим отсюда один из интегралов, стоящих в правой части:
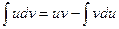
Полученная формула называется формулой интегрирования по частям.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде двух сомножителей u и dv, затем посленахождения v и du, используется формула интегрирования по частям. Иногда эту формулу приходится использоваться несколько раз.
Типы интегралов, которые удобно вычислять методом интегрирования по частям:
1) Интегралы вида
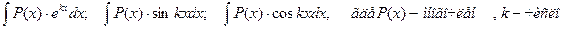
Удобно положить u=P(x), а за dv обозначить все остальные сомножители.
2) Интегралы вида
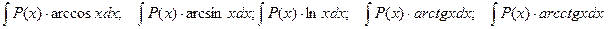
Удобно положить dv=P(x)dx, а за u обозначить все остальные сомножители.
3) Интегралы вида
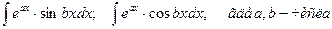
Удобно положить u=eax
Пример 1. Найти ∫xsinxdx.
Решение.
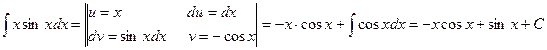
Пример 2. Найти ∫ xlnxdx.
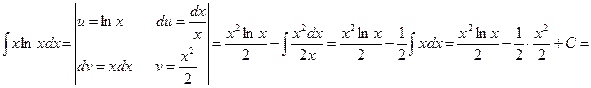
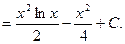
Пример 3. Найти 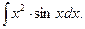
Решение.
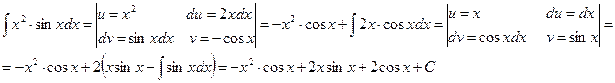
Пример 4. Найти 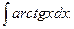
Решение.
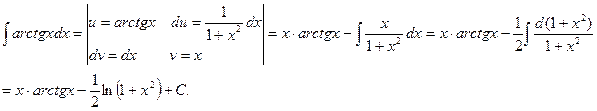
Нередко при вычислении интегралов использование повторного применения интегрирования по частям приводит снова к первоначальному интегралу. Получается уравнение, из которого и находится искомый интеграл. Такие интегралы принято называть возвратными
Пример 5. Найти 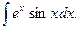
Решение.
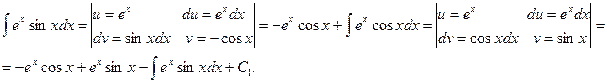
Решим уравнение относительно неизвестного интеграла:
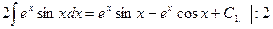
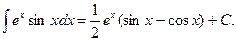
 2015-03-07
2015-03-07 10125
10125
