В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f; а, k, C - постоянные величины.
Дифференциал от неопределенного интеграла равен подынтегральному выражению
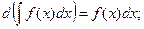
Производная неопределенного интеграла равна подынтегральной функции:
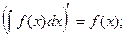
Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
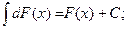
Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых:
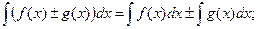
Постоянный множитель можно выносить за знак интеграла:
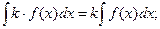
Инвариантность формулы интегрирования:
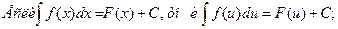
Таблица основных интегралов.
В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).
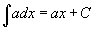
| 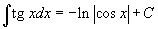
| ||
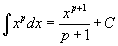
| 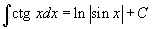
| ||
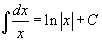
| 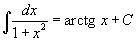
| ||
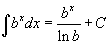
| 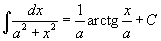
| ||
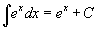
| 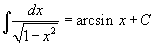
| ||
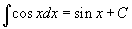
| 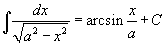
| ||
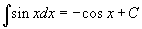
| 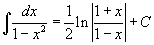
| ||
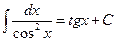
| 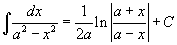
| ||
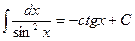
| 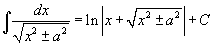
|
 2015-03-07
2015-03-07 606
606








