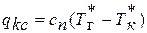 , где
, где 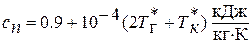 - средняя условная теплоемкость процесса подвода теплоты в камере сгорания
- средняя условная теплоемкость процесса подвода теплоты в камере сгорания
в) работа, развиваемая турбиной на её валу 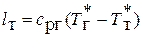 .
.
1.16. Уравнение неразрывности.
Рассматривается открытая термодинамическая система - поток жидкости или газа. Необходимо определить условия изменения массы рабочего тела при его течении в изолированном канале с твердыми стенками.
С этой целью выделим струйку тока из потока жидкости (рис.1.19) и два
нормальных сечения к её средней линии «1-1» и «2-2».
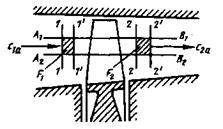 |
Рис.1.19. К выводу уравнения неразрывности.
За время 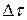 каждое из сечений перемещается и занимает положение «1’-1’» и «2’-2’». Определим массу газа между сечениями «1-1» - «1’-1’» и «2-2» - «2’-2’»:
каждое из сечений перемещается и занимает положение «1’-1’» и «2’-2’». Определим массу газа между сечениями «1-1» - «1’-1’» и «2-2» - «2’-2’»: 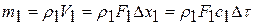 ;
; 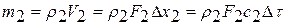
Принимаем, что поток стационарный, то есть изменение параметров потока не зависит от времени, а также равенство масс т 1 и т 2. Тогда разделив на 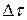 , получаем уравнение неразрывности
, получаем уравнение неразрывности 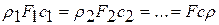
Подставляя размерности величин в эту формулу, получаем уравнение секундного расхода массы газа: 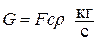
Из формулы для расхода газа следует, что он может уменьшиться, если:
а) уменьшается площадь проходного сечения F, например, при попадании посторонних предметов на вход в двигатель;
б) снижается скорость с, например, при увеличении угла атаки полета самолета уменьшается составляющая скорости полета на входе в двигатель;
в) уменьшается плотность 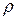 , например, при попадании горячих струй газа на вход в двигатель. В результате температура воздуха растет, а плотность падает согласно уравнению состояния
, например, при попадании горячих струй газа на вход в двигатель. В результате температура воздуха растет, а плотность падает согласно уравнению состояния 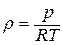 - «тепловое дросселирование».
- «тепловое дросселирование».
Разделив и умножив уравнение расхода на плотность тока при критическом режиме течения 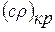 , получим уравнение расхода в следующем виде:
, получим уравнение расхода в следующем виде: 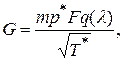
где 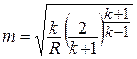 ;
; 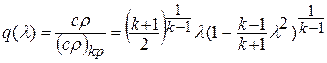 - относительная плотность тока. При умеренных температурах
- относительная плотность тока. При умеренных температурах 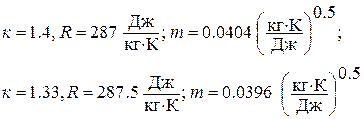
1.17. Уравнение первого закона термодинамики для открытой
 2015-03-27
2015-03-27 815
815








