Рассмотрим предварительно метод приближенного решения дифференциальных уравнений, обоснование которого будет дано в приведенной ниже теореме.
Метод Эйлера.







 Метод Эйлера заключается в том, что искомая интегральная кривая уравнения (16.2), проходящая через точку (х0, у0), заменяется ломаной, каждое звено которой касается интегральной кривой в одной из своих граничных точек (рис. 3).
Метод Эйлера заключается в том, что искомая интегральная кривая уравнения (16.2), проходящая через точку (х0, у0), заменяется ломаной, каждое звено которой касается интегральной кривой в одной из своих граничных точек (рис. 3).
у


h
h
y0 y1 y2
O x0 x1 x2 x
Рис. 3
Пусть требуется найти приближенное значение искомого решения при x = b. Разделим отрезок [ x0,b ] на п равных частей (полагаем, что b > x0) и назовем шагом вычисления h длину отрезка [ xi-1, xi ]. Заменим на отрезке [ x0, x1 ] интегральную кривую отрезком ее касательной в точке (х0, у0). Ордината этого отрезка при х = х1 равна y1 = y0 + hy0΄, где у0΄ = f(x0,y0). Так же найдем
y2 = y1 + hy1΄, где y1΄= f(x1,y1);
y3 = y2 + hy2΄, где y2΄= f(x2,y2);
..........................
yn = yn-1 + hy΄n-1, где y΄n-1 = f(xn-1,yn-1).
Можно предположить, что при 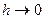 построенные таким образом ломаные Эйлера приближаются к графику искомой кривой. Доказательство этого утверждения будет дано в следующей теореме:
построенные таким образом ломаные Эйлера приближаются к графику искомой кривой. Доказательство этого утверждения будет дано в следующей теореме:
Теорема 16.1 (теорема существования и единственности решения). Если в уравнении
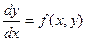
функция f(x,y) непрерывна в прямоугольнике D:
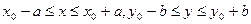 (16.5)
(16.5)
и удовлетворяет в D условию Липшица:
| f(x, y1) – f(x, y2) | ≤ N | y1 – y2 |, (16.6)
где N – постоянная, то существует единственное решение 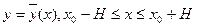 ,уравнения (16.2), удовлетворяющее условию (16.3), где
,уравнения (16.2), удовлетворяющее условию (16.3), где
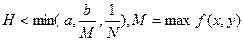 в D.
в D.
Замечание 1. Нельзя утверждать, что искомое решение будет существовать при 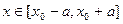 , так как интегральная кривая может выйти из прямоугольника (16.5), и тогда решение может быть не определено.
, так как интегральная кривая может выйти из прямоугольника (16.5), и тогда решение может быть не определено.
Замечание 2. Условие Липшица (16.6) можно заменить более сильным требованием 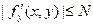 в D. Тогда по теореме Лагранжа
в D. Тогда по теореме Лагранжа 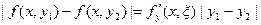 , где
, где  . Таким образом,
. Таким образом,  и
и  . Поэтому
. Поэтому 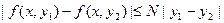 .
.
Доказательство теоремы 16.1.
Заменим уравнение (16.2) с начальным условием (16.3) эквивалентным интегральным уравнением 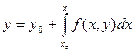 . (16.7)
. (16.7)
Легко проверить, что функция, обращающая в тождество уравнение (16.2), будет решением и уравнения (16.7).
Построим ломаную Эйлера у = уп(х), исходящую из точки (х0,у0) с шагом 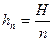 на отрезке [ x0, x0 + H ] (аналогично можно доказать существование решения на [ x0 – H, x0 ]). Такая ломаная не может выйти за пределы D, так как угловые коэффициенты каждого ее звена по модулю меньше М. Теперь докажем последовательно три утверждения:
на отрезке [ x0, x0 + H ] (аналогично можно доказать существование решения на [ x0 – H, x0 ]). Такая ломаная не может выйти за пределы D, так как угловые коэффициенты каждого ее звена по модулю меньше М. Теперь докажем последовательно три утверждения:
1) Последовательность у = уп(х) равномерно сходится.
2) Функция 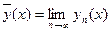 является решением интегрального уравнения (16.7).
является решением интегрального уравнения (16.7).
3) Решение 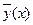 уравнения (16.7) единственно.
уравнения (16.7) единственно.
Доказательство 1). По определению ломаной Эйлера
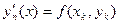 при
при 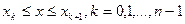 , или
, или 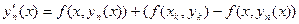 . (16.8)
. (16.8)
Обозначим 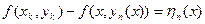 , тогда в силу равномерной непрерывности f(x) в D
, тогда в силу равномерной непрерывности f(x) в D 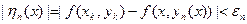 (16.9)
(16.9)
при 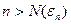 , где
, где 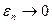 при
при 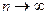 , так как
, так как 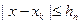 , а
, а 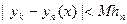 и
и 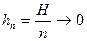 при
при 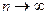 . Интегрируя (16.8) по х в пределах от х0 до х и учитывая, что
. Интегрируя (16.8) по х в пределах от х0 до х и учитывая, что 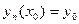 , получим:
, получим:
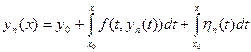 . (16.10)
. (16.10)
Так как п – любое целое положительное число, то для любого m > 0
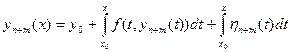 , откуда
, откуда
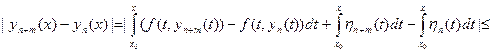
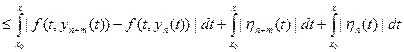 .
.
Тогда из (16.9) и условия Липшица следует, что
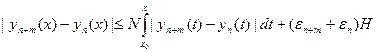 . Следовательно,
. Следовательно,
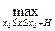
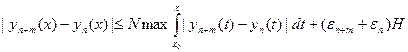 , откуда
, откуда
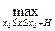
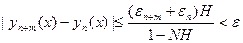
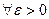 при
при 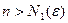 , то есть последовательность непрерывных функций уп(х) равномерно сходится при
, то есть последовательность непрерывных функций уп(х) равномерно сходится при 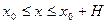 к непрерывной функции
к непрерывной функции 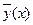 . Итак, утверждение 1) доказано.
. Итак, утверждение 1) доказано.
Доказательство 2). Перейдем в (16.10) к пределу при 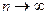 :
:
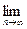
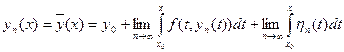 . (16.11)
. (16.11)
В силу равномерной сходимости уп(х) к 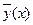 и равномерной непрерывности f(x,y) в D последовательность f(x,yn(x)) равномерно сходится к f(x,
и равномерной непрерывности f(x,y) в D последовательность f(x,yn(x)) равномерно сходится к f(x, 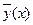 ). Действительно,
). Действительно, 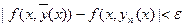 при
при 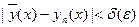 , что выполняется при
, что выполняется при 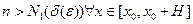 .
.
Следовательно, возможен переход к пределу под знаком интеграла. Учитывая, что 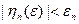 , где
, где 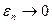 при
при 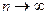 , получим из (16.11):
, получим из (16.11):
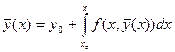 ,
,
то есть 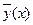 удовлетворяет уравнению (16.7). Утверждение 2) доказано.
удовлетворяет уравнению (16.7). Утверждение 2) доказано.
Доказательство 3). Предположим, что существуют два различных решения уравнения (16.7) у1(х) и у2(х), то есть 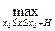 | y1(x) – y2(x) | ≠ 0. Тогда, подставляя эти функции в (16.7) и вычитая полученные равенства друг из друга, получим:
| y1(x) – y2(x) | ≠ 0. Тогда, подставляя эти функции в (16.7) и вычитая полученные равенства друг из друга, получим:
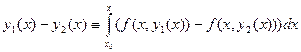 , откуда
, откуда
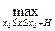 | y1(x) – y2(x) | =
| y1(x) – y2(x) | = 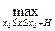
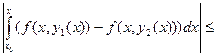
≤ 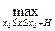
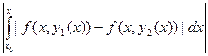 .Применим к этому неравенству условие Липшица:
.Применим к этому неравенству условие Липшица: 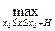 | y1(x) – y2(x) |≤ N
| y1(x) – y2(x) |≤ N 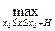
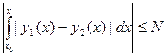
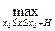 | y1(x) – y2(x) |
| y1(x) – y2(x) | 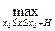
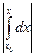
= NH 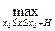 | y1(x) – y2(x) |. Если
| y1(x) – y2(x) |. Если 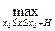 | y1(x) – y2(x) | ≠ 0, то полученное равенство:
| y1(x) – y2(x) | ≠ 0, то полученное равенство: 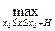 | y1(x) – y2(x) | ≤ NH
| y1(x) – y2(x) | ≤ NH 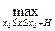 | y1(x) – y2(x) | противоречиво, так как по условию теоремы
| y1(x) – y2(x) | противоречиво, так как по условию теоремы 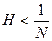 . Следовательно,
. Следовательно, 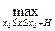 | y1(x) – y2(x) | = 0, то есть у1(х) ≡ у2(х).
| y1(x) – y2(x) | = 0, то есть у1(х) ≡ у2(х).
 2015-03-27
2015-03-27 581
581