Линеаризация диффе6ренциальных уравнений. Линейные дифференциальные уравнения высших порядков. Однородные уравнения, свойства их решений. Свойства решений неоднородных уравнений.
Определение 19.1. Линейным дифференциальным уравнением п -го порядка называется уравнение, линейное относительно неизвестной функции и ее производных:
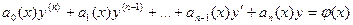 . (19.1)
. (19.1)
Если 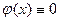 , уравнение называется линейным однородным.
, уравнение называется линейным однородным.
Если а 0(х) не равно нулю ни в одной точке некоторого отрезка [ a,b ], линейное однородное уравнение удобно записывать в форме
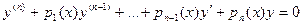 (19.2)
(19.2)
или 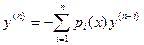 . (19.2′)
. (19.2′)
Замечание 1. Если коэффициенты pi (x) непрерывны на [ a,b ], то в окрестности любых начальных значений при 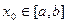 удовлетворяются условия теоремы суще6ствования и единственности.
удовлетворяются условия теоремы суще6ствования и единственности.
Замечание 2. Линейность и однородность уравнения сохраняются при любом преобразовании 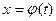 , где
, где 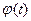 - п раз дифференцируемая функция и
- п раз дифференцируемая функция и 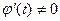 на [ a,b ], так как
на [ a,b ], так как 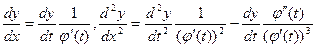 и т.д., то есть производная любого порядка по х является линейной однородной функцией производных по t.
и т.д., то есть производная любого порядка по х является линейной однородной функцией производных по t.
Замечание 3. Линейность и однородность уравнения сохраняются также при линейном однородном преобразовании неизвестной функции y(x) = α(x)z(x).
Определение 19.2. Назовем линейным дифференциальным оператором
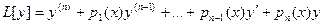 (19.3)
(19.3)
результат применения к функции у операций, задаваемых левой частью уравнения (19.2).
При этом уравнение (19.2) можно записать в виде L [ y ] = 0.
Свойства линейного дифференциального оператора.
1) Постоянный множитель выносится за знак линейного оператора: L [ cy ] = cL [ y ], так как (су)( i ) = cy ( i ).
2) L [ y1 + y2 ] = L [ y1 ] + L [ y2 ].
Действительно, (у1 + у2)( i ) = y1 ( i ) + y2 ( i ), откуда следует справедливость сформулированного свойства.
Следствие.
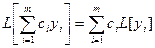 . (19.4)
. (19.4)
Используя свойства линейного оператора, можно указать некоторые свойства решений линейного однородного уравнения (19.2).
Теорема 19.1. Если у1 – решение уравнения (19.2), то и су1, где с – произвольная постоянная, – тоже решение этого уравнения.
Доказательство. Если L [ y1 ] = 0, то по свойству 1) линейного оператора L [ сy1 ] = 0, что и требовалось доказать.
Теорема 19.2. Сумма у1 + у2 решений уравнения (19.2) тоже является решением этого уравнения.
Доказательство. Так как L [ y1 ] = 0 и L [ y2 ] = 0, по свойству 2) линейного оператора L [ y1 + у2 ] = L [ y1 ] + L [ y2 ] = 0, что доказывает утверждение теоремы.
Следствие теорем 19.1 и 19.2. Линейная комбинация 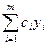 решений уравнения (19.2) у1, у2,…,ут с произвольными постоянными коэффициентами тоже является решением этого уравнения.
решений уравнения (19.2) у1, у2,…,ут с произвольными постоянными коэффициентами тоже является решением этого уравнения.
Если рассматривается линейное неоднородное уравнение (19.1), которое при 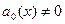 можно записать в виде
можно записать в виде
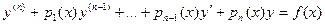 (19.5)
(19.5)
или L [ y ] = f(x), то при непрерывности функций pi (x) и f (x) оно имеет единственное решение, удовлетворяющее заданным начальным условиям (18.3).
Из свойств линейного оператора следуют свойства решений неоднородного линейного уравнения:
1) Сумма 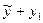 решения
решения 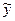 неоднородного уравнения (19.5) и решения у1 соответствующего однородного уравнения (19.2) является решением неоднородного уравнения (19.5). Доказательство.
неоднородного уравнения (19.5) и решения у1 соответствующего однородного уравнения (19.2) является решением неоднородного уравнения (19.5). Доказательство. 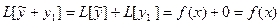 .
.
2) Если yi – решение уравнения L [ y ] = fi(x), то 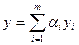 является решением уравнения
является решением уравнения 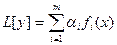 , где αi – постоянные (принцип суперпозиции или наложения). Доказательство.
, где αi – постоянные (принцип суперпозиции или наложения). Доказательство.
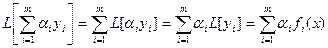 , что и требовалось доказать.
, что и требовалось доказать.
 2015-03-27
2015-03-27 284
284








