Рассмотрим два варианта этой теоремы. В любой электрической цепи без изменения токораспределения сопротивление можно заменить: 1) источником ЭДС, ЭДС которого численно равна падению напряжения на заменяемом сопротивлении и направлена встречно току в этом сопротивлении; 2) источником тока J, ток которого численно равен току в этом сопротивлении и имеет то же направление, что и ток I.
Для доказательства теоремы компенсации выделим из схемы одну ветвь с сопротивлением R, по которой течет ток I, а всю остальную часть схемы условно обозначим прямоугольником (рис. 2.18,а).
Если в выделенную ветвь включить два одинаковых и противоположно направленных источника ЭДС E, ЭДС которых равна падению напряжения на сопротивлении R под действием тока I (Е = IR рис. 2.18,6), то ток I в цепи от этого не изменится. Убедимся, что разность потенциалов между точками а и с в схеме рис. 2.18,6 при этом равна нулю. Действительно,
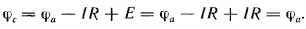
|
Если φc = φa, то точки а и с можно объединить в одну, т. е. закоротить участок ас и получить схему рис. 2.18, в. В ней вместо сопротивления R включен источник ЭДС Е.
1 Номер ветви соответствует индексу ЭДС. Схема, соответствующая второму варианту теоремы, изображена на рис. 2.18, г. Чтобы прийти к ней, заменим последовательно соединенные R и Е на участке ас (рис. 2.18, б) параллельным соединением источника тока J = E/R = I и сопротивления R. Так как
|
Uac = 0, то ток через R будет отсутствовать и потому R можно удалить из схемы. Если ЭДС E участка bc включить в состав источника тока, то получим схему рис. 2.18, г, где напряжение Uba = - IR
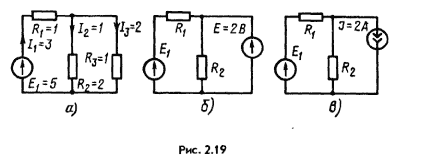
Пример 17. На схеме рис. 2.19, а даны значения R (Ом), ЭДС E1 (В) и токов I(А). Заменить R3 источником ЭДС и источником тока.
P е ш е н и е. На рис. 2.19, 6 изображена схема с источником ЭДС E = 2В, а на рис. 2.19, В — с источником тока J = 2А.
Назовем двухполюсником электрическую цепь, имеющую два зажима. Активный двухполюсник (А) содержит источники электрической энергии, пассивный (П) – нет.
Пусть через участок ab (рис. 1.20) под воздействием приложенного напряжения u за время dt проходит заряд dq. Поступающая при этом в приемник элементарная энергия
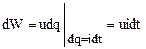 .
.
Тогда энергия, поступившая в приемник за промежуток времени от 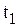 до
до 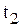 , равна
, равна
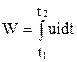 . (1.21)
. (1.21)
Для цепи постоянного тока
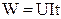 . (1.22)
. (1.22)
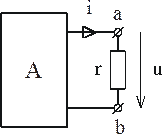
Рис. 1.20
Если образующие цепь проводники неподвижны (т.е. не совершается механическая работа), а ток постоянен, то работа сторонних сил источника энергии целиком расходуется на нагрев проводников (приемников). Количество теплоты, выделившееся при прохождении постоянного тока в проводнике с сопротивлением r за время t, определяется по закону Джоуля – Ленца
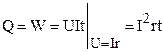 . (1.23)
. (1.23)
Производная энергии по времени (или скорость поступления энергии в цепь в данный момент времени) представляет собой мгновенную мощность
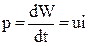 . (1.24)
. (1.24)
Мгновенная мощность – величина алгебраическая. Её значение положительно при одинаковых знаках напряжения и тока на зажимах активного двухполюсника (говорят, источник отдает энергию в цепь) – рис. 1.21а, и отрицательно при разных знаках (энергия возвращается из рассматриваемого участка цепи в источник) – рис. 1.21б.

а) б)
Рис. 1.21
В частном случае сопротивления r (рис. 1.6) мгновенная мощность
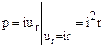 . (1.25)
. (1.25)
В цепи постоянного тока
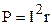 . (1.26)
. (1.26)
Величина мощности, рассеиваемой в сопротивлении, всегда положительна, т.к. протекание тока по проводнику сопровождается необратимым процессом преобразования электрической энергии в теплоту.
 2015-03-27
2015-03-27 608
608








