2015-03-27
1145
Рассмотрим изолированную систему. Тогда в изолированной системе, находящейся в равновесном состоянии или в случае происходящих обратимых процессов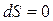 
.
Рассмотрим случай, когда в изолированной системе происходит необратимый процесс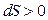 
. Такой процесс будет сопровождаться ростом энтропии.
Покажем, что переход теплоты от горячего тела к холодному происходит в соответствии со вторым законом термодинамики.
Пусть имеются два тела (первое разогретое, второе холодное), при этом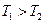 
. Установим между ними тепловой контакт.
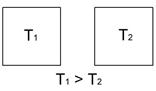Гипотетически возможны 2 случая:
1) Некоторое количество теплоты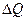 
переходит от горячего тела к холодному.
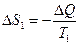(т. к. произошло понижение количества теплоты первого тела), 
.
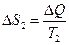Изменение энтропии в целом:
;
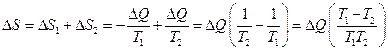2) 
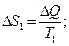
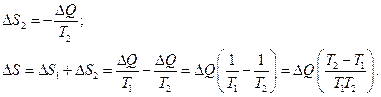
Соотнесем эти выражения со вторым законом термодинамики:
в первом случае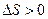 
, а во втором 
.
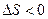Следовательно, первый процесс соответствует второму закону термодинамики.
Пусть имеется сосуд с газом. Этот сосуд разделен на две половинки, причем газ изначально находится в одной половинке.
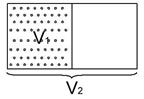
Убираем перегородку, и газ самопроизвольно заполняет весь объем.
Мы предположили, что обмена энергией с окружающей средой не происходит. Поэтому внутренняя энергия не меняется.
Энтропия – это функция состояния, поэтому неважно, каким путем система пришла в новое состояние. Можно предположить, что процесс происходил изотермически.
При изотермическом расширении газа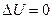 
. Тогда:
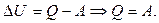
Воспользуемся уравнением Менделеева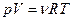 
:
.
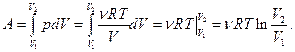
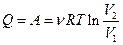Тогда согласно второму закону термодинамики:
.
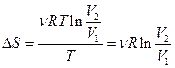Допустим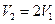 
:
.
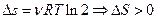Процесс расширения газа соответствует второму закону термодинамики, энтропия системы при этом возрастает.
Обратный процесс сопровождался бы уменьшением объема, который занимает газ. Но тогда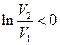 
, а, следовательно, приращение энтропии отрицательно, а это противоречит второму закону термодинамики.
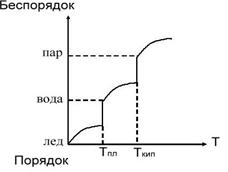
Увеличение энтропии в системе сопровождается увеличением хаоса и уменьшением порядка.
Это отражает диаграмма:
