Аппарат квантовой механики описывает вероятность нахождения частицы в некоторой области пространства в некоторый момент времени с помощью волновой функции 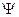 - вероятность того, что частица, находящаяся в некотором объеме
- вероятность того, что частица, находящаяся в некотором объеме 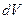 в некоторый момент времени
в некоторый момент времени 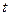 , определяется с помощью квадрата модуля волновой функции.
, определяется с помощью квадрата модуля волновой функции.
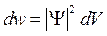 .
.
Таким образом, квантовая механика по самой своей сути носит статистический характер, т. е. глубинно связана со статистической физикой.
В отличие от классической физики в квантовой модели проявляется ряд специфических закономерностей. Выделим наиболее важные из них:
1. В квантовой механике выполняется принцип неопределенности Гейзенберга, согласно которому 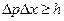 ,
, 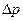 и
и 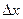 - неопределенности в задании импульса и координаты.
- неопределенности в задании импульса и координаты.
а) Из этого принципа вытекает, что классическое понятие траектории движения частицы в квантовой не выполняется.
б) Две частицы, находящиеся в некотором замкнутом объеме, принципиально различить невозможно.
При движении частиц, и попытке наблюдать эти частицы, неизбежно наступает момент, когда расстояние между частицами окажется сравнимым с 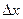 , т. е. с неопределенностью в задании координаты, и, начиная с этого момента, мы теряем идентификацию частиц.
, т. е. с неопределенностью в задании координаты, и, начиная с этого момента, мы теряем идентификацию частиц.
Этот принцип называется принципом тождественности квантовых частиц.
2. В классической физике значения физических величин, описывающих поведение частицы, таких как энергия, импульс, момент импульса носят непрерывный характер, т. е. с течением времени изменяются непрерывно.
В квантовой физике эти величины могут принимать только разрешенный набор дискретных значений. Так возможные значения энергии получаются из решения уравнения Шредингера.
С учетом того, что рассматривается идеальный одноатомный квантовый газ, выражение для энергии газа можно записать
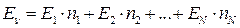 ,
,
Где 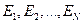 - те значения энергии, которые могут быть у частиц.
- те значения энергии, которые могут быть у частиц.
Для всех частиц этот набор одинаков, полученный из уравнения Шредингера, 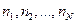 - число частиц, который в данный момент времени имеют соответствующие значению энергии.
- число частиц, который в данный момент времени имеют соответствующие значению энергии.
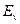 - энергия системы в некоторый момент Z.
- энергия системы в некоторый момент Z.
С течением времени значение Е у частиц изменится. Это будет соответствовать другому состоянию с другим заполнением квантовых уровней.
Вероятность того, что система находится в состоянии 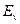
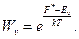
F* - свободная энергия квантовой системы.
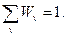
Сумма вероятностей нахождения системы в различных состояниях = 1:
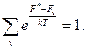
Вынесем 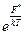
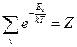 - аналогично интеграл состояния называется статистической суммой.
- аналогично интеграл состояния называется статистической суммой.
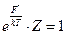
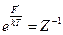
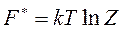
Если спектр энергетических значений состоит из очень большого числа близко расположенных значений уровней, то
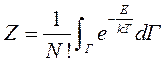
В силу того, что квантовые частицы неразличимы, число состояний по сравнению с классическим газом уменьшается в N! раз.
В силу принципа неопределенности 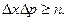 если распишем dГ как было в классической модели.
если распишем dГ как было в классической модели.
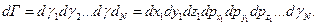
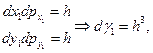 но таких произведений N штук получим
но таких произведений N штук получим 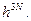
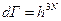 - min возможный объем в пространстве Г, в пределе которого можно выделить конкретное состояние системы (оно будет отличатся от состояния, находящееся в соседнем элементарном объеме).
- min возможный объем в пространстве Г, в пределе которого можно выделить конкретное состояние системы (оно будет отличатся от состояния, находящееся в соседнем элементарном объеме).
В случае классической модели 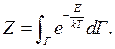 dГ – будет связано с произвольными действиями деления объема на число частиц, в этом был определенный произвол.
dГ – будет связано с произвольными действиями деления объема на число частиц, в этом был определенный произвол.
Число состояний изменится за счет уточнения (определения) выбора min фазового объема, который является 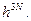
Поэтому в окончательном виде в квантовой модели
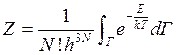
 2015-03-27
2015-03-27 329
329








