Лекция 5. 1. Формулировка второго начала термодинамики

1. Формулировка второго начала термодинамики. Энтропия.

2. Математическое выражение второго начала термодинамики. Энтропия обратимого и необратимого процессов.

3. Объединенное уравнение первого и второго начала термодинамики.

4. Энтропия как вероятность нахождения системы в данном состоянии. Статистический характер второго начала термодинамики.

Все процессы, которые можно себе представить, могут быть разделены на положительные, отрицательные и равновесные (квазистатические).

Положительными называются процессы, протекающие самопроизвольно: например, переход теплоты от горячего тела к более холодному, диффузия вещества из концентрированного раствора в разбавленный, т.е. любой процесс, приближающий систему к состоянию термодинамического равновесия.

Процессы, наблюдаемые в природе, протекают самопроизвольно лишь в одном направлении. Это необратимые процессы. Они идут без затраты работы. Более того, с помощью этих процессов можно получить работу.

Процессы, обратные положительным, которые могут идти лишь при затрате энергии извне или в сопряжении с положительными процессами внутри системы, называют отрицательными. В результате отрицательного процесса система удаляется от состояния равновесия.

Равновесные процессы занимают пограничное положение между положительными и отрицательными процессами, так как проходят через ряд непрерывных равновесных состояний системы.

Первого начала термодинамики недостаточно для полного описания термодинамических процессов. Оно позволяет точно найти энергетический баланс этих процессов, но не дает никаких указаний о направлении протекания и возможности протекания этих процессов. Так, при помощи первого начала термодинамики мы можем энергетически просчитать тепловой эффект любой воображаемой реакции, даже, если она неосуществима ни при каких условиях. Но пойдет ли такая реакция и в каком направлении, опираясь только на первое начало термодинамики, предсказать нельзя.

Так, первому началу термодинамики не противоречит разложение воды на водород и кислород при комнатной температуре, или же разложение углекислого газа, или самопроизвольное разделение раствора на его составляющие компоненты.

На вопрос о том, пойдет ли данный процесс, например, химическая реакция, самопроизвольно и какими параметрами будет характеризоваться система, когда в ней установится термодинамическое равновесие, можно получить ответ с помощью второго закона термодинамики.

Исторически второе начало термодинамики было сформулировано гораздо раньше первого и у М.В. Ломоносова "Холодное тело В, погруженное в теплое тело А, не может воспринять теплоту большую, чем которую имеет тело А".

Первая математическая формулировка была сделана Сади Карно (1824) в результате анализа работы паровых машин, дальше второе начало термодинамики получало более точные и строгие формулировки. Наиболее известными считаются следующие:

1. Постулат Клаузиса (1850): Теплота сама собой не может переходить от холодного тела к горячему, тогда как обратный переход протекает самопроизвольно. (Теплота не может самопроизвольно переходить от более холодного тела к более горячема).

2. Постулат Томпсона: "Теплота наиболее " холодного из участвующих в процессе тел не может служить источником работы." Или:

Различные виды работы стремятся перейти в теплоту, а теплота, в свою очередь, стремится рассеяться, т.е. распределиться между всеми телами наиболее равномерным образом."

Эти два постулата можно объединить в один:

отрицательный процесс не может быть единственным результатом цикла.

Наряду с отрицательным должен идти и положительный процесс, который является источником энергии для проведения отрицательного процесса.

Постулаты Клаузиса и Томпсона нельзя доказать, они подтверждены опытом и тем обстоятельством, что не известны случаи, которые противоречили бы этим постулатам.

Подобно тому, как первое начало термодинамики вводит понятие функции состояния - внутренней энергии, второе начало (работы Клаузиса) вводит понятие новой функции состояния – энтропии.

Согласно второму началу, в то время как внутренняя энергия изолированной системы остается неизменной, ее энтропия во всех самопроизвольных процессах увеличивается.

Чтобы логически понять и математически представить второе начало термодинамики, необходимо раскрыть смысл энтропии.

Большинство процессов представляет собой два одновременно происходящих явления: передачу энергии и изменение в упорядоченности расположения частиц относительно друг друга. Частицам (молекулам, ионам, атомам) присуще стремление к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное.

Так, если, например баллон с газом соединить с сосудом, то газ из баллона будет распределяться по всему объему сосуда. При этом система из более упорядоченного состояния (т.е. с меньшим беспорядком) переходит в состояние менее упорядоченное (с большим беспорядком). Газ в этом примере самопроизвольно расширяется, но самопроизвольно не сжимается, так как при сжатии естественное хаотическое движение молекул должно превратиться в направленное движение, что невозможно без вмешательства извне. При этом газ, расширяясь, передает энергию в виде теплоты и этот процесс самопроизвольный, естественный и необратимый.

Таким образом, можно сделать вывод, что протекание самопроизвольных процессов сопровождается рассеиванием тепловой энергии. (диссипацией)

Чтобы процесс рассеивания энергии характеризовать количественно, потребовалась термодинамическая функция, которая показывала бы, как изменяется рассеивание энергии при переходе системы из одного состояния в другое.

Эту функцию ввел Клаузис (1865) назвал энтропией (энтропос – обращенная внутрь) и обозначил буквой S.

Количественной мерой беспорядка (неупорядоченности) системы и является энтропия S.

Увеличение энтропии связано с усилением хаотического движения молекул. Следовательно, рост энтропии связан с увеличением неупорядоченности в системе.

Итак,:При переходе системы из более упорядоченного в менее упорядоченное состояние энтропия возрастает ΔS>0.

Переход же системы из менее упорядоченного в более упорядоченное состояние связан с уменьшением энтропии ΔS<0.

Понятно, что в приведенном примере маловероятно, чтобы газ сам собой собрался в баллоне, самопроизвольное протекание подобного процесса мало вероятно.

Соответственно степень беспорядка у вещества в газообразном состоянии больше, чем в жидком, а тем более – в кристаллическом. Например, стандартная энтропия у льда – 23 Дж/град моль, воды S= 69, 96 Дж/град моль, а у пара – 188, 74 Дж/град моль. У вещества в аморфном состоянии энтропия больше, чем в кристаллическом по той же причине.

2. Математическое выражение второго начала термодинамики. Энтропия обратимого и необратимого процессов.

Математическое выражение для энтропии Клаузис получил из цикла Карно, на котором основана работа тепловой машины.

Рабочее тело (1 моль идеального газа) получает от нагревателя с температурой Т₁ некоторое количество теплоты Q₁ и, расширяясь изотермически (кривая АВ), совершает работуА₁ Далее газ расширяется адиабатно, без подвода тепла (кривая ВС) и его температура падает до Т₂. Совершаемая в этом процессе работа равна А₂.

Затем совершаются два процесса сжатия газа: изотермическое сжатие (кривая СD) при температуре Т₂ в результате которого газ отдает приемнику теплоту Q₂ и адиабатное сжатие (кривая ДА) с повышением температуры газа до Т₁.В процессах сжатия над газом производится работа А ₃ и А ₄ соответственно. Все эти процессы обратимы.

В цикле Карно, как и в любом циклическом процессе, ΔU=0.

При проведении цикла рабочее тело получило количество теплоты

Q₁ – Q₂ и произвело работу А = А₁ – А₃ (так как А₂= А₄) (применяя закон Бойля и уравнение адиабаты заменяем V₄|V₃ на V₂|V₁)

Эффективность цикла оценивается коэффициентом полезного действия:

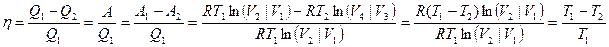Отсюда

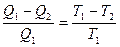
Учитывая, что Q₂ отдается газом теплоприемнику и ей следует приписать отрицательный знак, получим

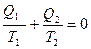
Отношение Q|T называют приведенной теплотой процесса. Как видно, сумма приведенных теплот в обратимом цикле Карно равна 0.

Любой произвольный процесс можно представить как сумму бесконечно малых циклов Карно, и для каждого бесконечно малого цикла можно написать:

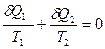
Тогда для конечного цикла общая сумма

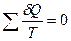
а в пределе мы можем написать ее как интеграл по замкнутому контуру:

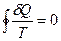
А если интеграл, взятый по замкнутому контуру, равен 0, то существует функция состояния, полный дифференциал которой равен подынтегральной величине. Эта функция состояния и является энтропией S.

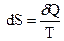
Данное уравнение является аналитическим выражением второго закона термодинамики для любого произвольного обратимого процесса.

Теперь рассмотрим перевод системы из начального состояния в конечное двумя путями: обратимым и необратимым.

В обоих процессах изменение внутренней энергии должно быть одинаковым, так как U – фу нкция состояния.

Известно, что при обратимом процессе совершаемая системой работа будет больше, чем при необратимом, т.е.

δА_обр> δА_необр

следовательно,

δQ_обр> δQ_необр

и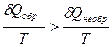

и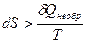

Тогда математическое выражение для энтропии в общем виде будет

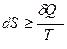
где знак неравенства относится к необратимым процессам, а знак равенства – к обратимым.

Так как энтропия является функцией состояния, то изменение ее не зависит от пути процесса, а зависит только от конечного и начального состояния системы:

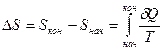
Так как энтропия является экстенсивным свойством системы, то если массу системы увеличить в n раз, то и значение энтропии увеличится в n раз.

Энтропия вещества зависит от его природы и массы, а также от температуры.

Единицей измерения является Дж/(моль*К).

3.Объединенное уравнение первого и второго начала термодинамики.

Подставляя значение δQ в выражение для первого закона термодинамики, получаем:

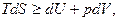
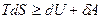
это уравнение объединяет первое и второе начала термодинамики и является фундаментальным уравнением термодинамики. Из него следует, что S является функцией U и V.

3. Энтропия как вероятность нахождения системы в данном состоянии. Статистический характер второго начала термодинамики.

В приведенном выше примере с газом понятно, что самопроизвольное расширение газа более вероятно, чем самопроизвольное его сжатие. Количественно связь энтропии с термодинамической вероятностьюW нахождения данной системы в данном состоянии выражают с помощью уравнения Больцмана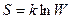

где k – постоянная Больцмана.

Из этого уравнения следует, что чем больше энтропия системы, тем больше вероятность нахождения системы в данном состоянии. Увеличение энтропии в самопроизвольных процессах указывает пути наиболее вероятного их осуществления в изолированной системе.

Поэтому второй закон термодинамики можно рассматривать как закон вероятности, применимый к системам, состоящим из большого числа частиц, т.е. к макросистемам, свойства которых складываются из свойств микросистем. Чем больше в макросистеме число микросистем, изменяющихся в определенном направлении, тем наиболее вероятным становится это направление процесса для всей макросистемы. В то время как в системах, состоящих из малого числа частиц возможны и менее вероятные процессы из-за флуктуаций В этом заключается статистический характер второго закона термодинамики.