Второго закона термодинамики

СТАТИСТИЧЕСКИЙ ХАРАКТЕР

План лекции: Статистический характер второго закона термодинамики. Термодинамическая вероятность состояния системы. Уравнение Больцмана-Планка. Границы применимости второго закона термодинамики.

Второй закон термодинамики можно назвать законом возрастания энтропии при самопроизвольном процессе в изолированной системе. В связи с этим очень важно выяснить физические причины необратимости реальных процессов, сопровождающихся возрастанием энтропии.

Смысл второго закона термодинамики можно понять более глубоко исходя из молекулярно-кинетической теории. Рассмотрим уравнение 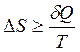. В него входят такие параметры, как температура и теплота. Температура является мерой интенсивности теплового движения молекул; теплота – неупорядоченная форма обмена энергии между различными частями системы вследствие хаотического движения частиц. Следовательно, возрастание энтропии в самопроизвольных процессах отражает закономерные изменения в молекулярно-кинетическом состоянии системы.

Характер зависимости энтропии идеального газа от температуры и давления показывает, что энтропия S, может служить мерой беспорядка в расположении и движении молекул. Возрастание энтропии связано с самопроизвольным переходом вещества из состояния со строго упорядоченным расположением частиц в состояние с большим и наибольшим молекулярным беспорядком. Максимальной энтропии отвечало бы состояние газа с совершенно равномерным распределением хаотически движущихся частиц по объему. Однако, в каждый момент времени, в результате беспорядочного движения молекул, имеются местные отклонения от равномерного распределения: временное увеличение концентрации молекул в одних участках объема и уменьшение в других. Поэтому можно говорить о более или менее вероятных состояниях системы. Термин «вероятность состояния» равнозначен по смыслу понятию «беспорядок». Энтропия, является мерой вероятности состояния системы. Это открытие способствовало развитию статистической термодинамики.

Макросостоянием системы называется состояние, заданное термодинамическими параметрами. Это состояние из большого числа частиц. Микросостояние – это непосредственно ненаблюдаемое состояние молекул, атомов, ионов и др. частиц, характеризуемое координатами их положения в пространстве и скоростью их движения. В статистической термодинамике при подсчете вероятности состояния исходят из того, что одно макросостояние системы, например газа, при определенной температуре и давлении, может быть осуществлено большим числом микросостояний с любым распределением частиц по координатам и скоростям. Поскольку частицы газа постоянно и хаотически движутся, микросостоянияпостоянно чередуются. Однако любое микросостояние равновероятно. Число микросостояний, определяющих данное макросостояние, называется термодинамической вероятностью состояния системы.

Допустим, что имеется всего три молекулы (обозначим цифрами), которые размещаются в двух ячейках фазового пространства (обозначим клетками). Рассмотрим макросостояние, когда в одной ячейке имеется 2 молекулы, а в другой одна. Данное макросостояние реализуется тремя перестановками молекул между ячейками, то есть тремя микросостояниями:

первое микросостояние

второе микросостояние

третье микросостояние

Если в системе находится N молекул, то общее число перестановок будет N!. Поделив N! на число перестановок N_i! в каждой ячейке и исключив их тем самым из подсчета, получим термодинамическую вероятность:

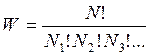, (7.1)

где - число молекул в каждой фазовой ячейке, причем N=N₁+N₂+N₃+…

Процесс выравнивания микросостояний, идущий в естественных условиях самопроизвольно и с возрастанием энтропии, приводит к росту термодинамической вероятности. Термодинамическая вероятность характеризует ту или иную степень беспорядка в сообществе частиц, из которых состоят тела системы. Термодинамическая вероятность, или вероятность состояния системы, оценивается энтропией.

Связь между энтропией и термодинамической вероятностью указывает статистическую природу второго закона термодинамики. Больцман Л. сделал допущение, что энтропия есть некоторая функция вероятности, S = f (W). В классической термодинамике доказывается, что в самопроизвольном процессе энтропии возрастает. С точки зрения статистической термодинамики этот же процесс сопровождается возрастанием вероятности W. При равновесии S и W принимают свои максимальные значения. Вид функции S = f (W) определяется уравнением Больцмана-Планка:

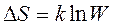. (7.2)

Константа Больцмана k должна иметь размерность энтропии.

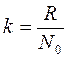, (7.3)

здесь N₀ – число Авогадро, равное 6,02 10²³.

Границы применимости второго закона термодинамики. Статистический характер второго закона термодинамики приводит к заключению, что увеличение энтропии в самопроизвольных процессах указывает на наиболее вероятные пути развития процессов в изолированной системе. Невозможность процесса следует принимать лишь как его малую вероятность по сравнению с обратным. Поэтому второй закон термодинамики нужно рассматривать как закон вероятности. Он тем точнее соблюдается, чем больше размеры системы.

Действие второго закона нельзя распространять на микросистемы. Но также неправомерно распространять второй закон на вселенную. Второй закон термодинамики применим лишь к изолированной системе ограниченных масштабов. Вселенная же существует неограниченно во времени и пространстве.