Из определения интегрирующего множителя имеем
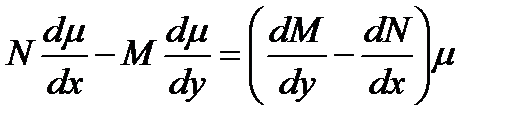 (10.20)
(10.20)
или же, деля обе части равенства (10.20) на 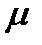 ,
,
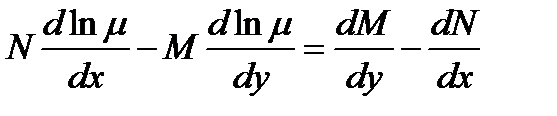 (10.20’)
(10.20’)
Мы получили в виде (10.20) или (10.20’) уравнение в частных производных для определения неизвестной функции 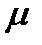 . Задача интегрирования такого уравнения в общем случае не проще, чем задача решения уравнения (10.6). Конечно, нам достаточно знать только одно частное решение уравнения (10.20) иногда по каким-нибудь особенностям уравнение (10.20), удается найти такое частное решение, и тогда интеграция уравнения (10.6) сводится к квадратуре.
. Задача интегрирования такого уравнения в общем случае не проще, чем задача решения уравнения (10.6). Конечно, нам достаточно знать только одно частное решение уравнения (10.20) иногда по каким-нибудь особенностям уравнение (10.20), удается найти такое частное решение, и тогда интеграция уравнения (10.6) сводится к квадратуре.
Рассмотрим, например, случай, когда существует интегрирующий множитель, являющийся функцией одного только х.
В этом случае 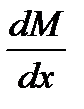 = 0 и уравнение (10.20') обращается в такое
= 0 и уравнение (10.20') обращается в такое
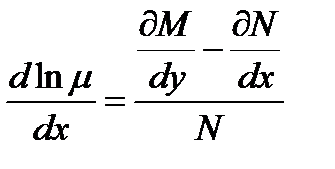 (10.21)
(10.21)
Ясно, что для существования интегрирующего множителя, не зависящего от у необходимо и достаточно, чтобы правая часть была функцией одного х, в таком случае 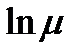 найдется квадратурой:
найдется квадратурой:
Пример 10.6: ( 2ху+ х2у+ 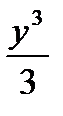 )dх+(х2+ у2)dу = 0
)dх+(х2+ у2)dу = 0
Здесь
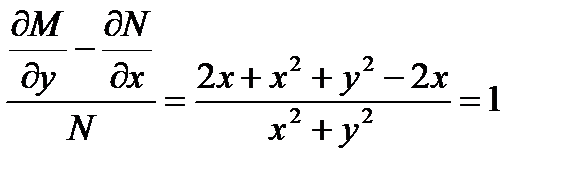
Следовательно, 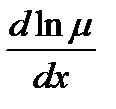 = 1,
= 1, 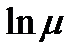 = х,
= х, 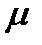 = ех
= ех
Уравнение
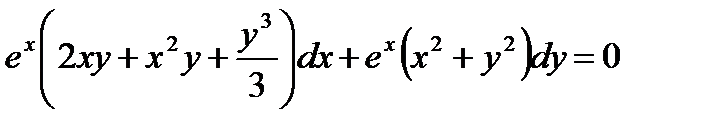
есть уравнение в полных дифференциалах. Интегрируем его,
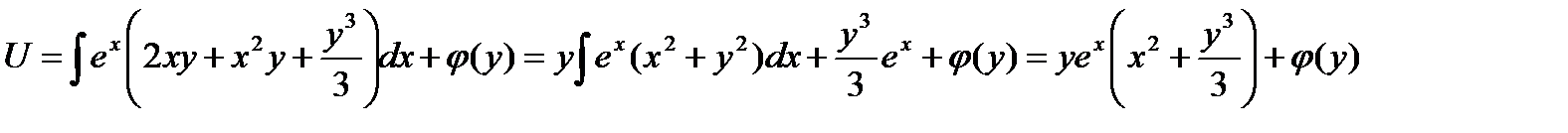
Для нахождения 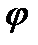 (у) вычислим
(у) вычислим 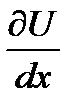 и приравняем его
и приравняем его 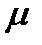 N
N
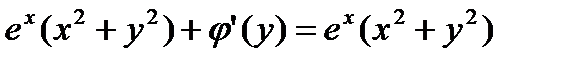
Откуда 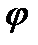 '(у) =0
'(у) =0
и общий интеграл нашего уравнения есть
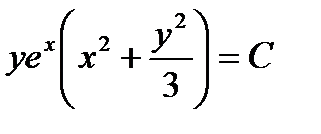
Рассмотрим частный случай интегрирующего множителя, зависящего только от x, когда N=1 в этом случае уравнение имеет вид
dy-f(x,y)dx=0 (10.22)
Уравнение (10.21) примет вид
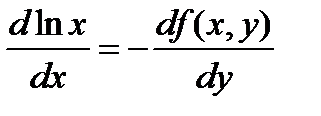 с условием, что
с условием, что 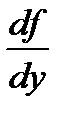 есть функция одного х.
есть функция одного х.
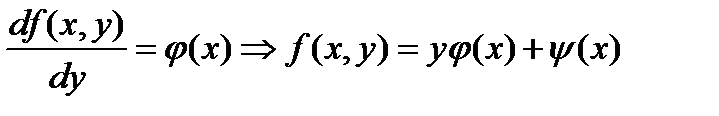
В таком случае f(х,у) имеет вид
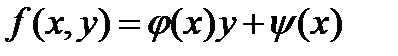
т.е. уравнение, написанное в виде (10.22) и допускающее интегрирующий множитель, зависящий только от х есть уравнение линейное.
Из уравнения (10.21) имеем
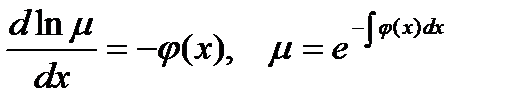
Переходя к обозначениям лекции 9 для линейного уравнения,приходим к заключению.
Линейное уравнение 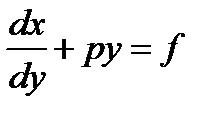 имеет интегрирующий множитель
имеет интегрирующий множитель 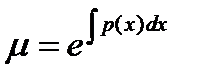
Пример10.7: Уравнение 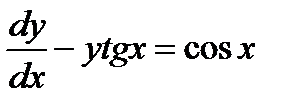 имеет интегрирующий
имеет интегрирующий
множитель 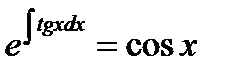 , умножая на него обе части уравнения, имеем
, умножая на него обе части уравнения, имеем

где левая часть есть полный дифференциал, интегрируя находим
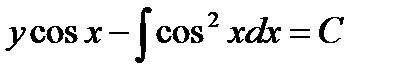
или
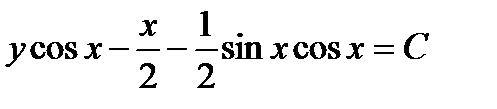 - общий интеграл.
- общий интеграл.
 2015-03-07
2015-03-07 1954
1954
