Сформулируем без доказательств одну из важнейших теорем дифференциальных уравнений, которая утверждает существование и единственность решения задачи Коши локально вблизи начальной точки х0.
Теорем 10.1. Пусть дано дифференциальное уравнение.
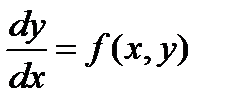 (10.1)
(10.1)
удовлетворяющее начальному условию
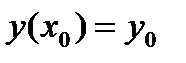 (10.2)
(10.2)
относительно функций 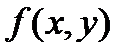 ..Мы предположим следующее
..Мы предположим следующее
А. Функция 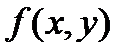 определена в прямоугольнике
определена в прямоугольнике
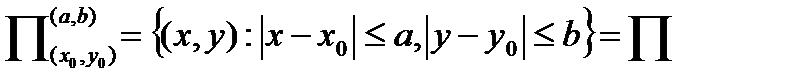
непрерывна в П, где 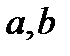 - постоянные числа.
- постоянные числа.
Так как непрерывная функция является в замкнутой области ограниченной, то из условия А следует существование такого положительного числа М, что имеет место неравенство
 (10.3)
(10.3)
В. Функция 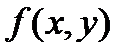 удовлетворяет условию Лифшица по у. То есть сущестсвует такое положительное число N, что для любого значения
удовлетворяет условию Лифшица по у. То есть сущестсвует такое положительное число N, что для любого значения
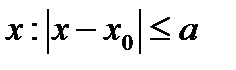 и
и 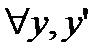 переменной
переменной 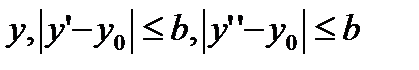 выполняется неравенство
выполняется неравенство
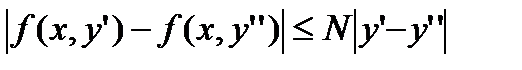 (10.31)
(10.31)
Тогда дифференциальное уравнение (10.1) имеет решение 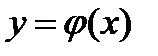 , удовлетворяющее условию (10.2) и определенное в промежутке
, удовлетворяющее условию (10.2) и определенное в промежутке 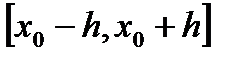 , где
, где 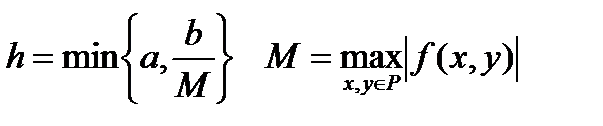
Это решение единственно в том смысле, что любое другое решение 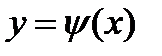 уравнение (10.1), удовлетворяющее тому же начальному условию (10.2)
уравнение (10.1), удовлетворяющее тому же начальному условию (10.2)
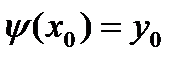
совпадает с 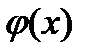 в том же промежутке, где оба решения определены одновременно.
в том же промежутке, где оба решения определены одновременно.
§ 2. Особые точки
1. Исследуем уравнение (10.1), в случае когда нарушается условие теоремы существования и единственности.
Пусть не выполняется условие А. Допустим, что в окрестности точки (х0, у0) функция f(х, у) является неограниченной.
Первый случай. 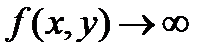 когда
когда 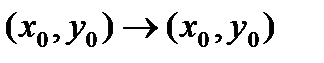 . Тогда функция
. Тогда функция
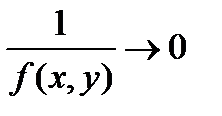 примет ее значения равным 0 в точке (х0, у0).
примет ее значения равным 0 в точке (х0, у0).
Рассмотрим уравнение 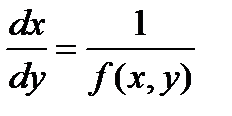
и предположим, что для нее условия теоремы Коши в окрестности точки (х0, у0) выполнены, мы получим интегральную кривую, проходящую через точку (х0, y0), уравнение ее будет иметь вид
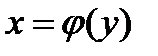
при х = х0, у = у0 имеем 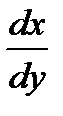 = 0. Таким образом, интегральная кривая
= 0. Таким образом, интегральная кривая
имеет в точке (х0, у0) вертикальную касательную.
Пример 10.1. 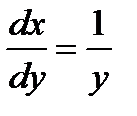 при х = х0, у = у0=0 функция не ограничена, но в уравнении
при х = х0, у = у0=0 функция не ограничена, но в уравнении 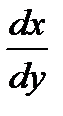 = у правая часть при этих начальных данных обращается в нуль. Искомое решение: у2 = 2 (х - х0) - парабола с вертикальной касательной при х = х0.
= у правая часть при этих начальных данных обращается в нуль. Искомое решение: у2 = 2 (х - х0) - парабола с вертикальной касательной при х = х0.
Второй случай. 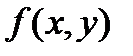 является неограниченной в окрестности точки (х0, y0) не имеет единственного предела
является неограниченной в окрестности точки (х0, y0) не имеет единственного предела 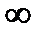 , когда точка (х, у) стремится к (х0, y0) между тем как в остальных точках этой
, когда точка (х, у) стремится к (х0, y0) между тем как в остальных точках этой
окрестности или 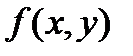 или
или 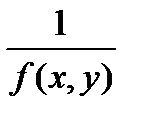 непрерывна. Такова, например,
непрерывна. Такова, например,
функция 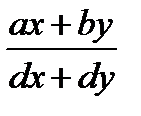 в окрестности точки х=0, у=0. В самом деле, когда
в окрестности точки х=0, у=0. В самом деле, когда
точка (х, у) стремится к (0, 0), оставаясь на прямой ах + bу = 0, эта функция равна 0. Если же точка (х, у) лежит на прямой сх + dу = 0, функция не определена (нуль в знаменателе), но вблизи этой прямой она бесконечно велика; по другим направлениям функция имеет другие предельные значения. Мы скажем, что в точке (0, 0) наша функция имеет изолированную особую точку типа 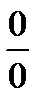 .
.
 2015-03-07
2015-03-07 533
533








