Всякое уравнение первого порядка, разрешенное относительно производной
у'=f(х,у) (10.4)
или в дифференциальном виде
dу-f(х,у)dх = 0 (10.5)
или в симметричном виде
М(х,у)dх + N(х,у)dу = 0 (10.6)
Рассмотрим частный случай, когда левая часть уравнения (10.6) представляет полный дифференциал некоторой функции V(х, у)
М (х, у)dх + N (х, у)dy = 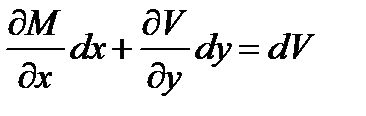
В этом случае уравнение (10.6) называется уравнением в полных точных дифференциалах.
Последнее тождество равносильно двум:
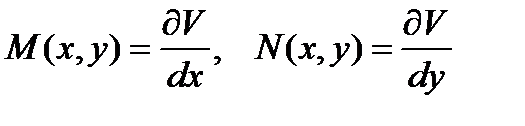 (10.7)
(10.7)
Если в (10.6) подставить вместо у решение уравнения (10.1), то мы
будем иметь dV(х,у)=0, откуда
V(х.у) = С (10.8)
Для значений x и у, соответствующих этому решению (С -постоянное) и обратно, для функции у, определяемой уравнением 10.8) имеем dV=0. Итак, уравнение (10.7), содержащее произвольное постоянное, является интегралом уравнения (10.6) в полных дифференциалах.
Для существования решения у(х) дифференциального уравнения (10.1), принимающего при х=x0 значения у0 достаточно, чтобы уравнение (10.8) определяло у как неявную функцию от х, т.е. чтобы в точке (х0, y0)
мы имели 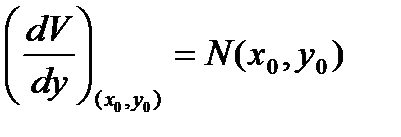 . В таком случае решение у(х), проходящее через точку (х0,у0) определяется из уравнения:
. В таком случае решение у(х), проходящее через точку (х0,у0) определяется из уравнения:
V(х,у) = V(х0,y0)
Если N (х0, у0) = 0, а М (х0, у0) 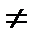 0, то соотношение (10.6) определяет х как функцию от у; исключение в смысле существования и единственности решения составляют только точки, в которых М (х0, y0) = N (x0,y0) = 0; это особые точки уравнения (10.6) [П. 2]
0, то соотношение (10.6) определяет х как функцию от у; исключение в смысле существования и единственности решения составляют только точки, в которых М (х0, y0) = N (x0,y0) = 0; это особые точки уравнения (10.6) [П. 2]
Найдем признак, по которому для данного уравнения (10.6) судят, принадлежит ли оно к классу уравнений в точных дифференциалах. Из равенства (10.7), предполагая существование соответствующих производных, получаем
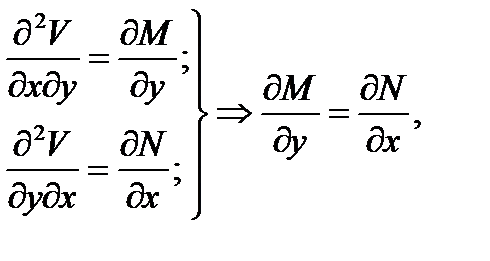 (10.9)
(10.9)
который является необходимым условием полного дифференциала.
Покажем, что условие (10.9) является также достаточным, а именно, предполагая его выполненным, найдем функцию V(х, у), удовлетворяющую соотношениям (10.7). Мы имеем 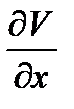 = М(х,у), откуда интегрируя по x от х0 до x: и считая у постоянным, получаем
= М(х,у), откуда интегрируя по x от х0 до x: и считая у постоянным, получаем
V(х,у) = 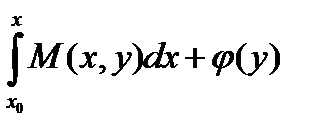 (10.10)
(10.10)
Заметим, что (10.10) удовлетворяет 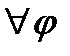 первому соотношению (10.7). Покажем, что при выполнении условий (10.9) можно найти функцию
первому соотношению (10.7). Покажем, что при выполнении условий (10.9) можно найти функцию 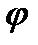 (у), чтобы выполнялось и второе соотношение (10.7). Примем правило дифференцирования интеграла по параметру из (10.10), имеем
(у), чтобы выполнялось и второе соотношение (10.7). Примем правило дифференцирования интеграла по параметру из (10.10), имеем
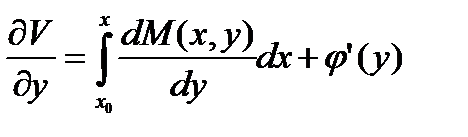
тогда в силу (10.9), получаем
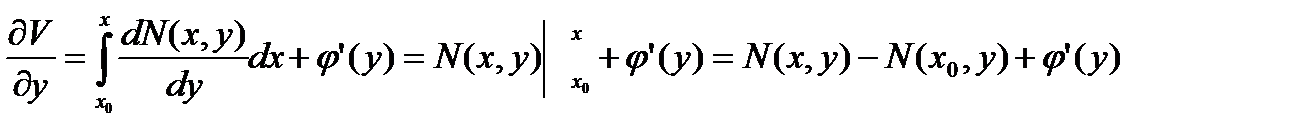
Тогда, учитывая, что 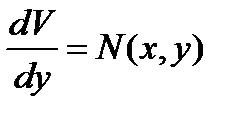 , получим
, получим 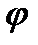 '(у) = N(x0,у)
'(у) = N(x0,у)
Определим
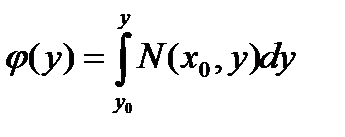 (10.11)
(10.11)
Равенство (10.11) подставляя в (10.10), находим
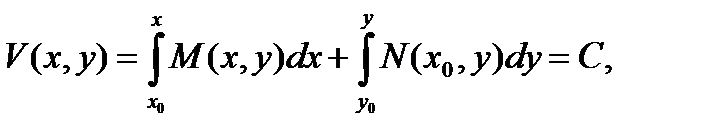 (10.12)
(10.12)
которое является общим интегралом уравнения (10.5).
Примечание: На практике оказывается проще дифференцировать равенство (10.10) по у и, заменяя 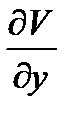 известной функцией N(х,у) определить из полученного равенства
известной функцией N(х,у) определить из полученного равенства 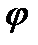 '(у), а затем найти
'(у), а затем найти 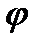 квадратурой.
квадратурой.
Пример 10.5: Найти полный интеграл (Зх2+6ху2)dх+(6х2у+4у3)dу = 0
Решение: Здесь М(х,у)= (Зх2+6ху2); N(х,у)= (6х2у+4у3)
и 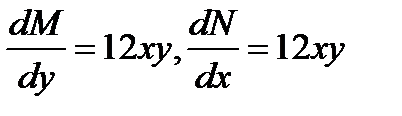 и условия (10.9.) выполнено
и условия (10.9.) выполнено
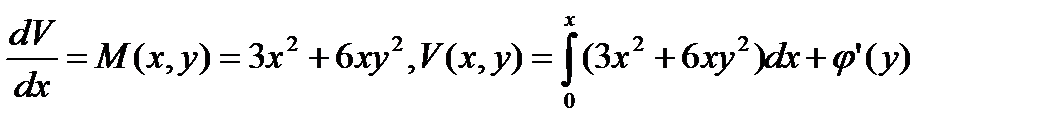
или
V(х,у) = (х3+3х2у2) + 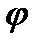 (у)
(у)
Вычислим 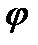 ’(у):
’(у):
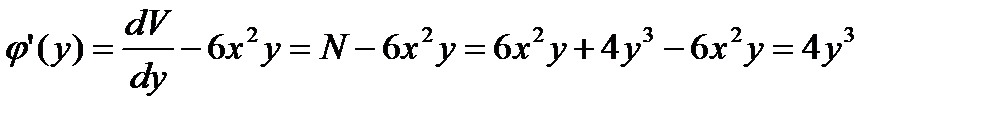
откуда 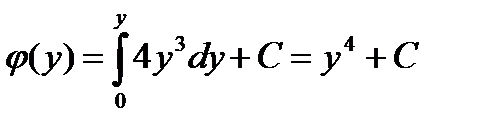
Таким образом, полный интеграл
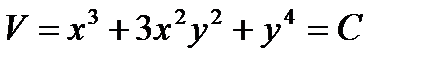
Если левая часть уравнения (10.6) не есть полный дифференциал, возникает вопрос – нельзя ли найти такую функцию 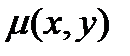 , по умножении на которую левая часть уравнения (10.6) станет полным дифференциалом некоторой функции
, по умножении на которую левая часть уравнения (10.6) станет полным дифференциалом некоторой функции 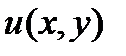 .
.
Такая функция 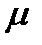 называется интегрирующим множителем. Таким образом,
называется интегрирующим множителем. Таким образом, 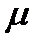 - интегрирующий множитель, мы имеем
- интегрирующий множитель, мы имеем
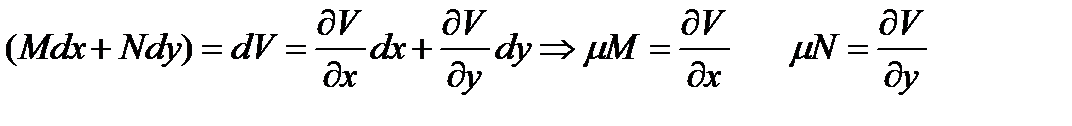 (10.13)
(10.13)
Первый вопрос: Для всякого ли уравнения первого порядка существует интегрирующий множитель? Из теоремы существования мы знаем, что при известных условиях уравнение (10.1) имеет общий интеграл
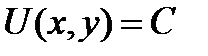
Дифференцируем это уравнение по х, полагая у=у(х), таким образом мы исключаем С и придем к дифференциальному уравнению
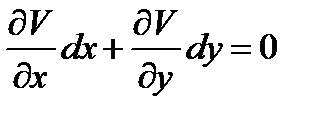 или
или 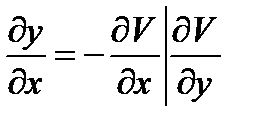 (10.14)
(10.14)
Это уравнение должно быть тождественно с исходным уравнением (10.6), которую мы находим в виде
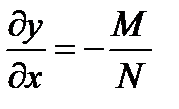 (10.15)
(10.15)
Сравнивая (10.14) и (10.15), имеем
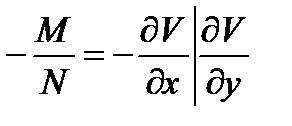 или
или 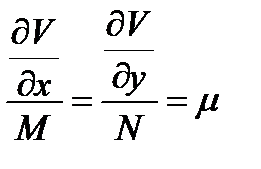
Из последних равенств имеем
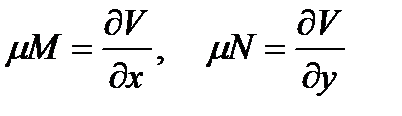 (10.16)
(10.16)
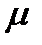 - является интегрирующим множителем. Итак, всякое дифференциальное уравнение первого порядка, удовлетворяющее некоторым условиям, имеет интегрирующий множитель.
- является интегрирующим множителем. Итак, всякое дифференциальное уравнение первого порядка, удовлетворяющее некоторым условиям, имеет интегрирующий множитель.
Число интегрирующих множителей данного уравнения бесконечно. В самом деле, пусть 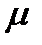 - есть какой-нибудь интегрирующий множитель уравнения (10.1), а
- есть какой-нибудь интегрирующий множитель уравнения (10.1), а 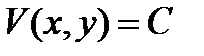 есть интеграл этого уравнения. тогда
есть интеграл этого уравнения. тогда 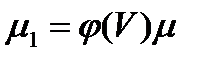 , где
, где 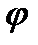 - произвольная дифференциальная функция, являющаяся также интегрирующим множителем. В самом деле, выражение
- произвольная дифференциальная функция, являющаяся также интегрирующим множителем. В самом деле, выражение
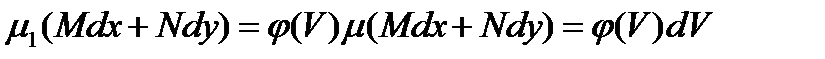
является полным дифференциалом от функции
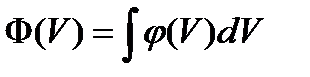
Следовательно,
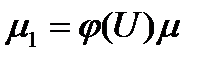 (10.17)
(10.17)
есть интегрирующий множитель уравнения (10.6) Докажем, что всякий интегрирующий множитель уравнения (10.6) дается формулой (10.17).
В самом деле, пусть кроме дифференцирующего множителя 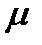 , имеется еще какой-то интегрирующий множитель
, имеется еще какой-то интегрирующий множитель 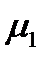 . Мы имеем
. Мы имеем
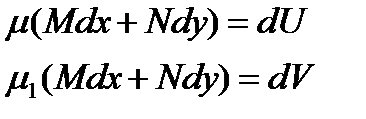 (10.18)
(10.18)
где V=V(х,у) раскрывая последние тождества, имеем
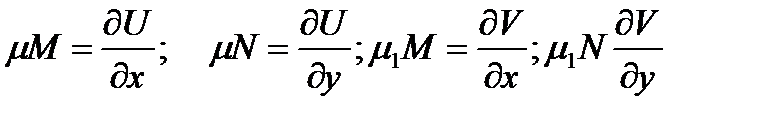
Откуда
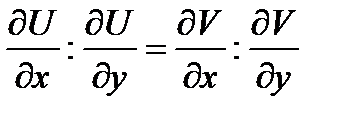 или
или 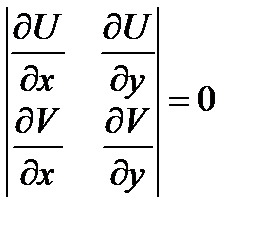
Таким образом, функции якобиян функции U и V тождественно равны нулю, а так как 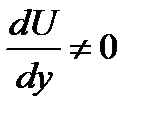 , то между этими функциями существует зависимость вида
, то между этими функциями существует зависимость вида
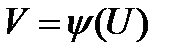 (10.19)
(10.19)
Равенство(10.8)даеттогда 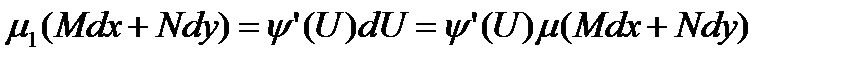
Откуда
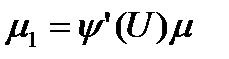
Следствие: Если известны два существенно различных интегрирующих множителя 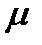 и
и 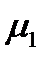 , уравнения (10.6), то общий интеграл получается без всякой квадратуры в виде
, уравнения (10.6), то общий интеграл получается без всякой квадратуры в виде 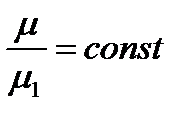
 2015-03-07
2015-03-07 1632
1632
