Доказательство. В самом деле, применим для доказательства критерий Коши.Пусть ε>0 произвольно мало

В самом деле, применим для доказательства критерий Коши.Пусть ε>0 произвольно мало. Так как числовой ряд 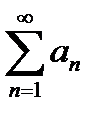сходится, то можно найти такое N, что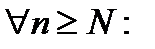

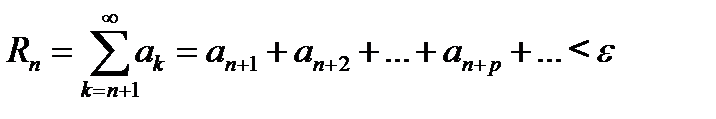
Тогда очевидно,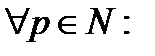

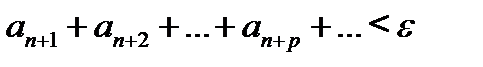
Оценим разность:

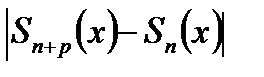
Где 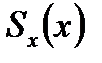-есть частичная сумма ряда 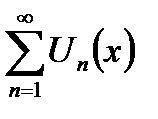имеем: 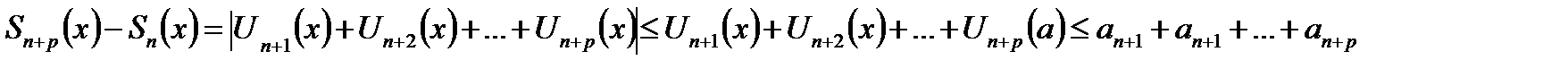Если теперь положить n≥N,то получим: 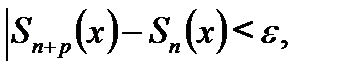если n≥N и 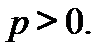Этим установлена равномерная сходимость ряда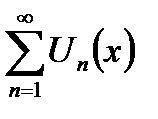

Абсолютная его сходимость следует из неравенства:

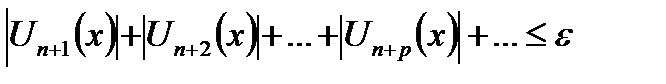
Примеры.18.4. Пусть дан ряд

1.

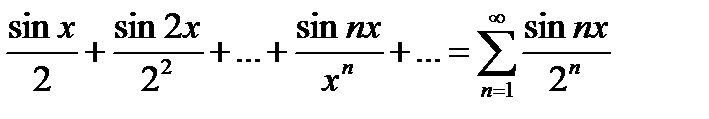
этот ряд равномерно сходится на всей абсциссе. В самом деле, каков бы ни был х, всегда

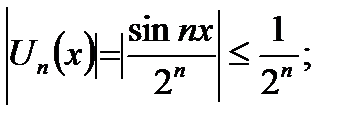
а ряд 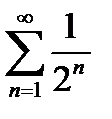-сходится.

2. 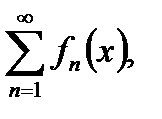где

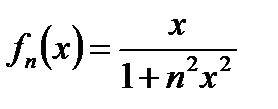
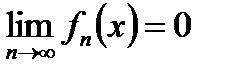
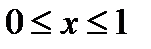
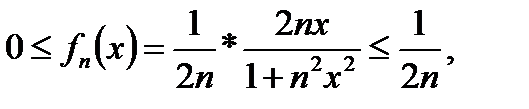ряд 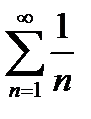расходящийся

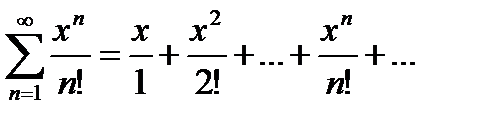
Этот ряд равномерно сходится на любом отрезке [-l,l].

Действительно,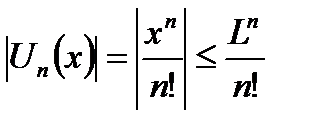

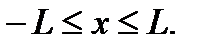
Ряд 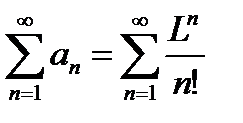-сходится.

3.

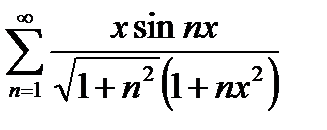
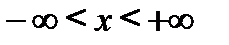
Очевидно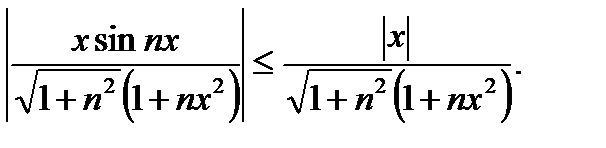

Учитывая, что 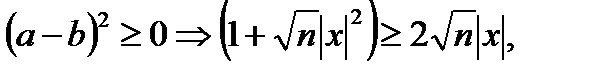имеем:

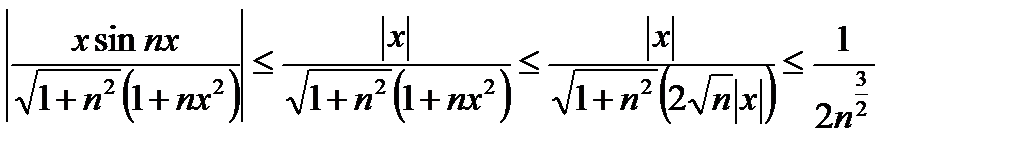
Так как ряд 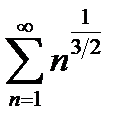сходится 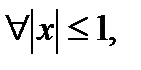следовательно данный ряд сходится равномерно.

Докажем теперь достаточный признак равномерной сходимости, применимый в отличие от признака Вейерштрасса и к неабсолютно сходящимся рядам. Его формулировка напоминает признак Дирихле для сходимости числовых рядов и впервые встречается в работах Харди.