Если:
1) Последовательность (18.1) имеет в 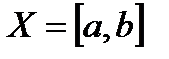 предельную функцию U(х):
предельную функцию U(х):
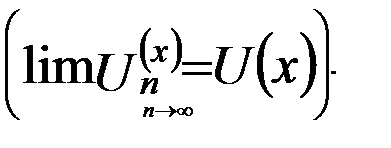
2) Для каждого числа ε>0 существует такой независящий от х номер N, что при n>N неравенство:
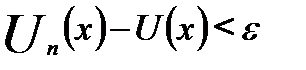
выполняется сразу для всех 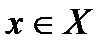 , то говорят, что последовательность (18.1) сходится к функции U(х) равномерно относительно х в области X.
, то говорят, что последовательность (18.1) сходится к функции U(х) равномерно относительно х в области X.
Определение 18.2'
Если:
1) Последовательность (18.1) имеет в X предельную функцию U(х).
2) 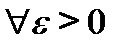 существует не зависящий от х номера N, что при n>N неравенство
существует не зависящий от х номера N, что при n>N неравенство 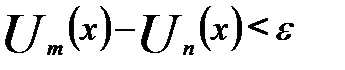 выполняется сразу
выполняется сразу 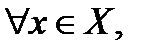 то говорят, что последовательность (18.1) сходится к функции
то говорят, что последовательность (18.1) сходится к функции 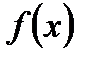 равномерно относительно х в области X.
равномерно относительно х в области X.
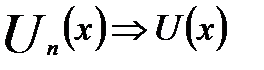
Говорят, что последовательность 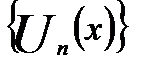 равномерно сходится на множестве Е, если существует функция U(х), удовлетворяющая условию:
равномерно сходится на множестве Е, если существует функция U(х), удовлетворяющая условию:
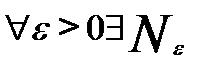
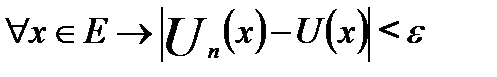
Пусть существует числовая последовательность 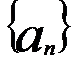 и номер
и номер 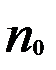 такие,что
такие,что
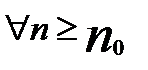
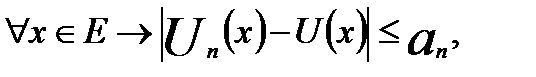
причем 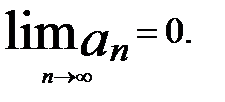 Тогда:
Тогда:
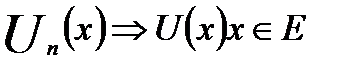
Примеры18.2. Доказать, что последовательность 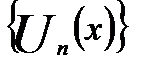 равномерно сходится на множестве Е и найти ее предельную функцию U(х), если:
равномерно сходится на множестве Е и найти ее предельную функцию U(х), если:
а) 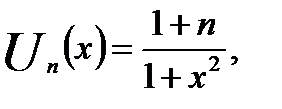
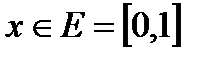
б) 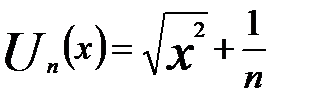 E=R
E=R
а) В этом случае 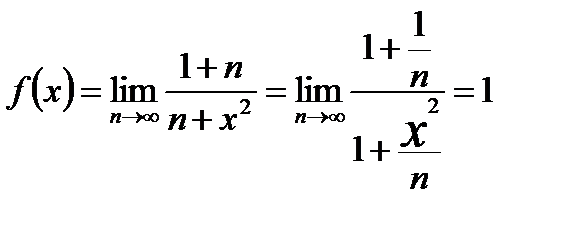 и
и
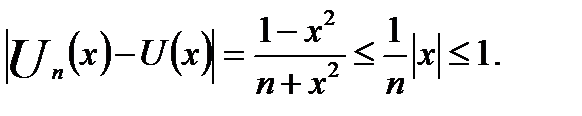
Следовательно, 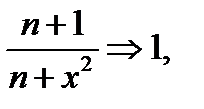
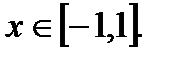
б) Используя неравенство 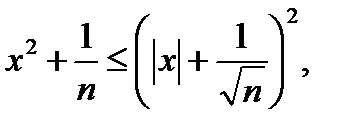 получаем:
получаем:
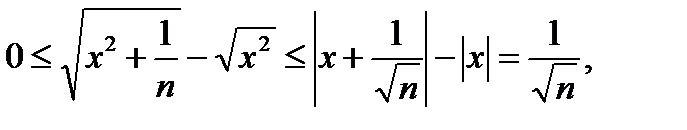 откуда следует, что
откуда следует, что
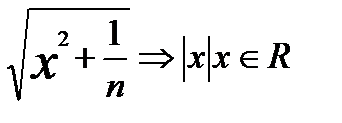
 2015-03-07
2015-03-07 410
410








