2015-03-07
423
1. Пусть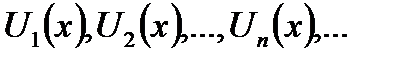 
последовательности функций, определенных на одном и том же отрезке или на каком- либо множестве.
Ряд
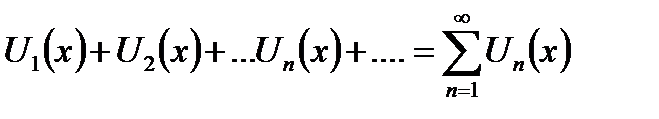(18.3)
называется функциональным рядом, а функцию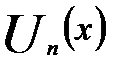 
n -м членом ряда. Обозначим частичные суммы ряда (18.3) через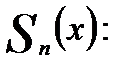 
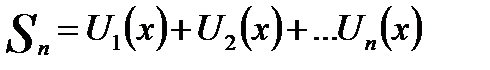
2. Сходимость функциональных рядов.
Определение 18.3. Функциональный ряд (18.3) называется сходящимся при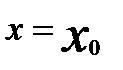 
или в точке 
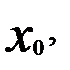если последовательность его частичных сумм
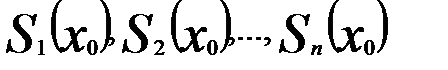(18.4)
сходится в этой точке, иными словами, если сходится числовой ряд:
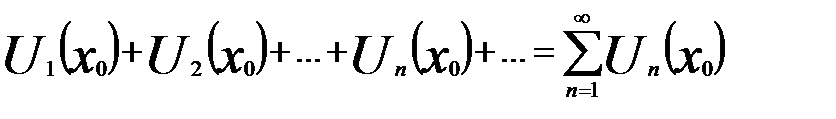(18.5)
Функциональный ряд, сходящийся в каждой точке некоторого множества, называется сходящимя на этом множестве.
Предел последовательности (18.4), то есть сумму (18.5) обозначим через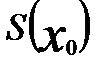 
и назовем суммой ряда (18.3) в точке 
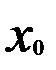. Сумма ряда, очевидно, представляет собой некоторую функцию от х, определенную во всех точках, где сходится ряд.
Пример18.3. Рассмотрим функциональный ряд
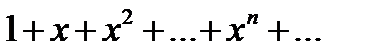
Этот ряд сходится при всех значениях х в интервале (-1,1). Так как по признаку Даламбера:
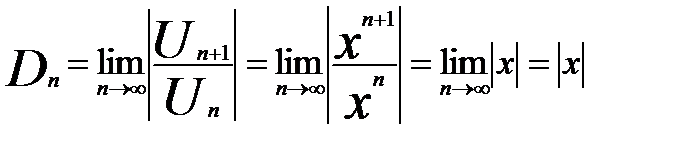
По признаку Даламбера, если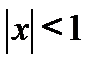 
ряд сходится, отсюда 1< x <1 
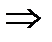(-1,1). Для каждого значения x в интервале (-1,1) сумма ряда равна 
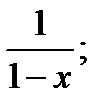(сумма убывающей геометрической прогрессии со знаменателем x). Таким образом, в интервале (-1,1), данный ряд определяет функцию:
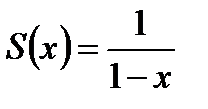
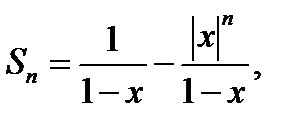
которая является суммой ряда, то есть:
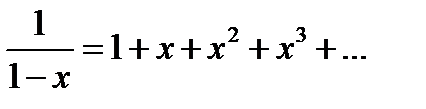
Функциональный ряд (18.4) называется абсолютно сходящимся в точке x, если сходится ряд, составленный из абсолютных его членов:
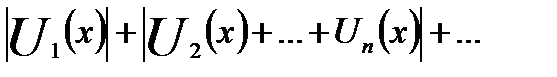
В силу определения сходимость функционального ряда сводится к сходимости последовательности функций. Обратно, если дана некоторая последовательность функций:
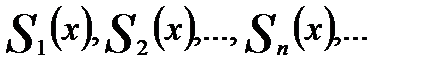
сходящаяся к функции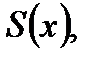 
то ряд:
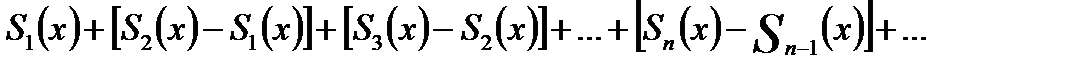
Сходится там же, где сходится последовательность
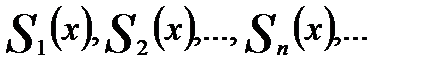и сумма ее равна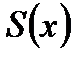 
Пусть 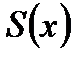-сумма ряда. Назовем остатком ряда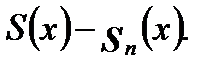 
Остаток ряда обозначим через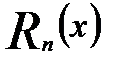 
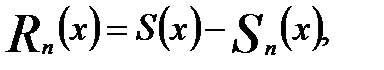
где
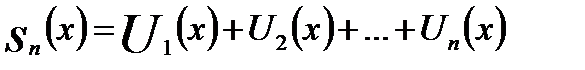
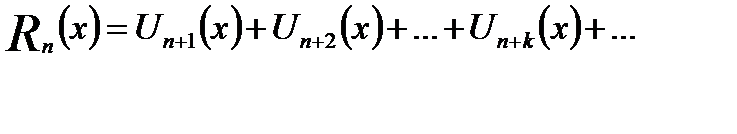
Для всех значений х в области сходимости ряда имеет места соотношение
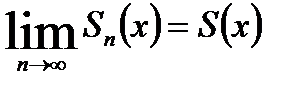Поэтому:
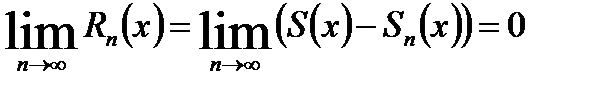
То есть остаток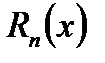 
сходящегося ряда стемится к нулю при n→∞.
