Теорема 18.5

Если функция 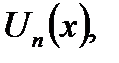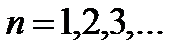- непрерывна в точке 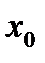множества 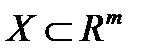и ряд 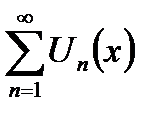равномерно сходится на Х, то сумма 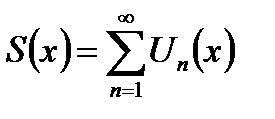также непрерывна в точке

Теорема 18.6. 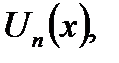n=1,2,3,…. непрерывны в точке 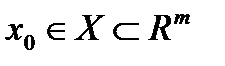.Если функция и 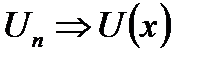то U непрерывна в точке .

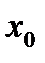Теорема 18.7. Пусть функции 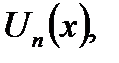n=1,2,3,…. непрерывны на отрезке [a,b] и ряд:

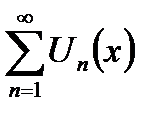(18.7)

равномерно сходится на [a,b]. тогда, каковы бы ни была точка 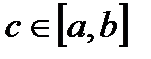ряд:

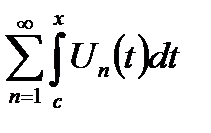(18.8)

также равномерно сходится [a,b], и если:

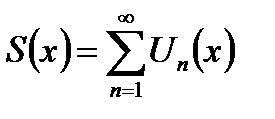(18.9)

то:

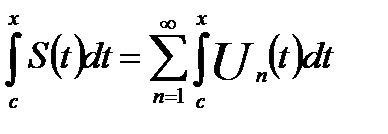
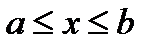(18.10)

Если эту формулу переписать в виде:

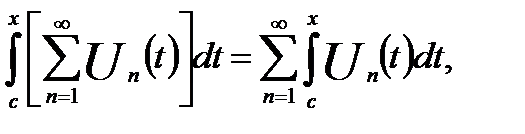
то видно, что она означает законность при условиях, перечисленных в последней теореме, почленного интегрирования ряда.

Доказательство. В силу равномерной сходимости ряда (18.7) и непрерывности его членов на отрезке [a,b], согласно теореме 18.6 его сумма поэтому она интегрируется на любом отрезке с концами в точках 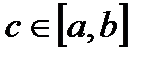и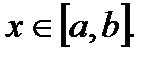

Покажем, что ряд (18.8) равномерно сходится на отрезке [a,b] к функции:

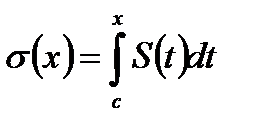(18.11)

Пусть:

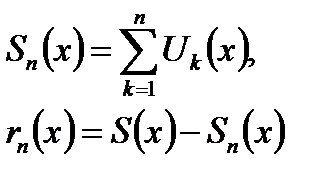
Обозначим через 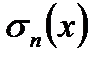частичные суммы ряда (18.8):

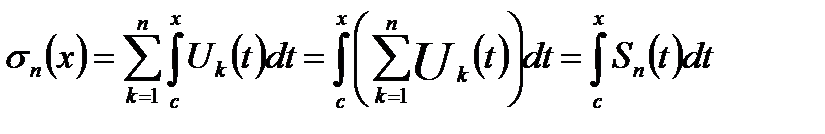
теперь для любого 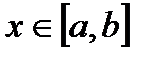имеем:

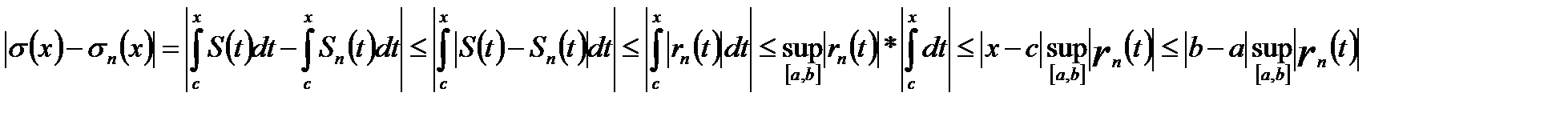
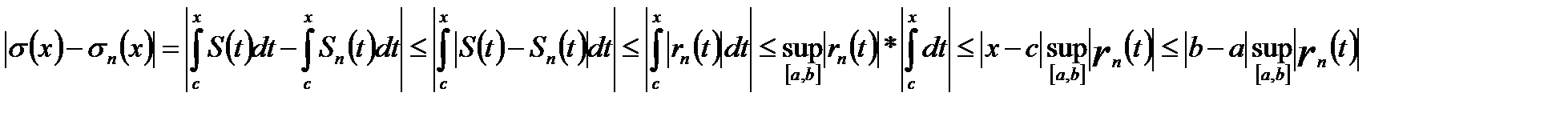(18.12)

Последовательность 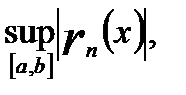n=1,2,3, Является числовой последовательностью. В силу равномерной сходимости ряда (18.7) имеем

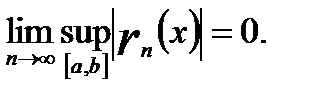
Поэтому из неравенства (18.12) вытекает утверждение теоремы.

Перефразируем полученный результат для последовательности функции.

Теорема 18.7'. Если последовательность непрерывных на отрезке [a,b] функций 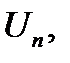n=1,2,3,…. На этом отрезке равномерно сходится к функци U, то каковы бы ни была точка 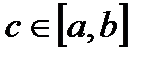то:

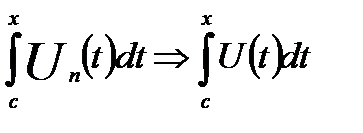на [a,b]

В частности,

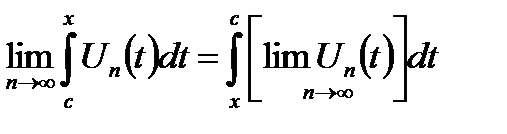
Рассмотрим теперь вопрос дифференцирования рядов.

Теорема 18.8. Пусть функции 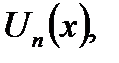n=1,2,3,…. непрерывно дифференцируемы на отрезке [a,b] и ряд, составленный из этих производных:

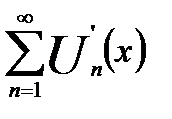(18.13)

равномерно сходится на отрезке [a,b]. Тогда, если ряд 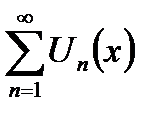сходится хотя бы в одной точке 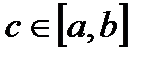, то он сходится на всем отрезке [a,b], его сумма:

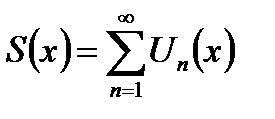(18.14)

непрерывно дифференцируема и:

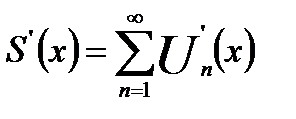(18.15)

если эту формулу переписать в виде:

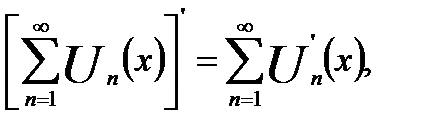
то видно, что она означает законность при сделанных предположениях почленного дифференцирования ряда.