Гиперболические функции

Функция shz и chz определяются формулами

shz= 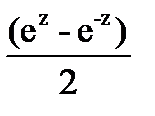, chz= 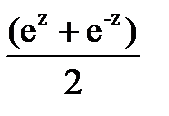(24.12)

Из (24.8) и (24.12) видно, что shz=-isin(z) ch(z)=icos(z).Таким образом, свойства функций shz и chz непосредственно вытекают из свойств функций sinz и cosz. Отметим, в частности, что функции shz и chz непрерывна во всей комплексной плоскости: все решения уравнения shz=0 находятся по формуле

z=k 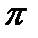i, k=0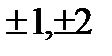

А все решения уравнения chz=0 находятся по формуле Z=(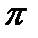 /2+k 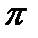)i, k=0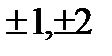

Функция thz, cthz определяются формулами

thz=shz/chz cthz=chz/shz

Надо отметить, что формулы для тригонометрических и гиперболических функций, справедливые при действительных Х, остаются в силе для комплексных Z