Тема:Дифференцирование комплексной функции. Условия Коши - Римана. Сопряженные гармонические функции. Понятие регулярной функции Эквивалентность условий Коши - Римана

§1.Дифференцирование комплексной функции.. Определение 25.1. Производная.

Пусть функция f(z) определена в некоторой окрестности точки Zo. Если существует конечный предел отношения

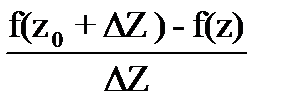при 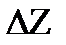, то этот предел называется производной f(z) в точке Zo и обозначается 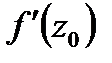, а функция f(z) называется дифференцируемой в точке z₀. Таким образом,

(25.1)

Функция f(z) называется дифференцируемой в области, если она дифференцируема в каждой точке этой области.

Пусть f =f(z₀+ 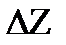)-f(z₀)

Тогда соотношение (25.1) примет вид

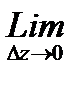
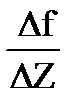= (z₀) (25.2)

Это означает, что для любого e>0 существует d=d(e)>0 такое, что неравенство

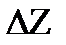, f=f^/ (z₀), +0(), ( )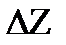

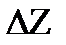
имеет место, если 0<| 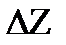|<d. Из (3,2) следует, что обратно, если приращение f функции f(z) представляется в виде

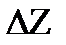f =A +d (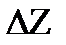) (25.3)

где А- комплексная постоянная, не зависящая от 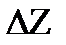, то функция f(z) дифференцируема в точке z₀ и А= (Zo).

Таким образом, равенство (25.3) является необходимым и достаточным условием дифференцируемости функции f(z) в точке Z₀. Из (25.3) в частности, следует, что функция, дифференцируемая в точке Z₀ непрерывна в этой точке.

Пример25.1. Функция f(z)=zⁿ (n>1-целое) дифференцируема во всей комплексной плоскости, так как

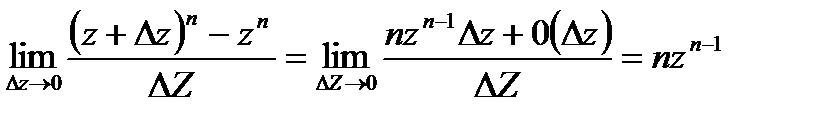(25.4)

Следовательно,

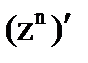= nz^n-1 (25.5)

Из определения производной и свойств пределов вытекает, что на функции комплексной переменной распространяются известные из курса математического анализа правила дифференцирования.

1. Если функции f(z) и g(z) дифференцируемы в точке z, то их сумма, произведения и частное (при g(z) 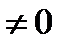) также дифференцируемы в этой точке и имеют место следующие формулы:

(f 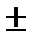g)¢=f ¢ 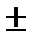g ¢,

(cf)¢=cf ¢ (c=const) (25.6)

() ¢= ¢,

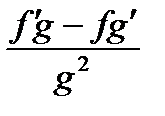2. Если функция f(z) дифференцируема в точке Z, а функция F(w) дифференцируема в точке W, W=f(z), то функция Ф(z)=F[f(z)] дифференцируема в точке Z, причем

(25.7)

Пример 25.2. Из формул (25.5) и (25.6) следует, что

А) функция f(z)=z^m, где m<0 – целое,

дифференцируема во всей комплексной плоскости, кроме точки z=0, и (z^m)¢=mz^m-1; в частности,

(z^-1) ¢=() ¢=-

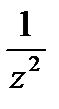
б) многочлен

P_n(z) =a₀z^ing+a₁z^ing-1+...+a_n-1z+a_n;

дифференцируем во всей комплексной плоскости функции и

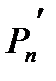(z)=na₀z^n-1+(n-1)a₁z^n-2+...+2a_n-2 z+a_n-1;

В) рациональная функция R(z)=Р_n(z)/Q_n(z) имеет производную во всех точках, где Q_m(z) 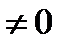, причем формулы для R(z) имеют тот же вид, что и соответствующие формулы для действительных х. В определении производной содержится требование, чтобы предел (3.1) не зависел от способа стремления 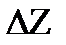к нулю. Мы раньше отметили, что непрерывность функции комплексной переменной f(z)=U(x,y)+iV(x,y) в точке z=x+iy равносильна непрерывности функции U и V в точке (x,y). Аналогичное утверждение не имеет место для дифференцируемости. Именно требование дифференцируемости функции f(z)= U +iV налагает дополнительные условия на частные производные функции U и V.