Число z= 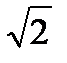 +i записать в показательной форме.
+i записать в показательной форме.
Решение: так как |Z|= 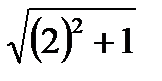 =
= 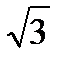 argZ=arctgy/x=arctg
argZ=arctgy/x=arctg 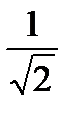 то по формуле (24.2.) можно записать
то по формуле (24.2.) можно записать 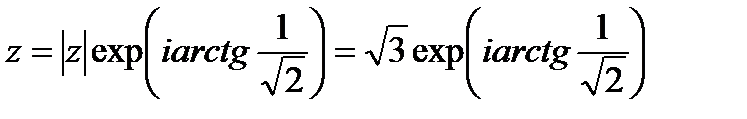
Пусть дано комплексноe число Z,Z 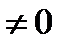 Z
Z 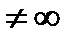
Число 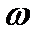 называется натуральным логарифмом числа Z,если е
называется натуральным логарифмом числа Z,если е 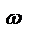 =Z
=Z
Все значения логарифма Z обозначают Lnz, найдем эти значения, если z=r(cos  +isin
+isin  ), а
), а 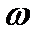 =u+iv то по определению логарифма
=u+iv то по определению логарифма
е u+iv=r(cos  +isin
+isin  )
)
или
еu (cosV+isinV)=r(cos  +isin
+isin  )
)
отсюда следует, еu=rV=argZ=argZ+2 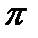 k k=0
k k=0 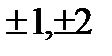 . Так как
. Так как 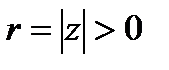 , то
, то 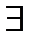 !
!
действительное значение 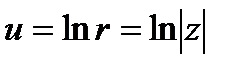 . Поэтому
. Поэтому 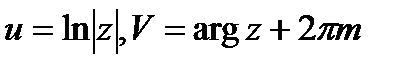 .
.
Таким образом, всякое комплексное число Z¹0, Z¹  имеет бесконечное множество значений натурального логарифма. Все они описываются формулой.
имеет бесконечное множество значений натурального логарифма. Все они описываются формулой.
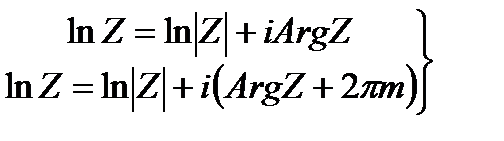 (*)
(*)
Однозначная функция lnZ=ln|Z|+iArgZ называется главным значением логарифма.
Пример.24.3. Найти все значения ln(1+i)
Решение. По формуле (*) находим
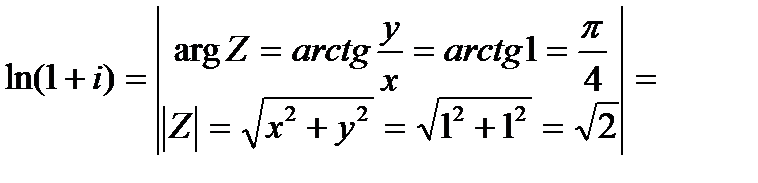
= 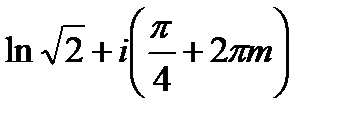 , m=0,
, m=0, 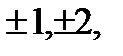
Если а действительно и а>0, то
Ln a =ln a +2 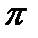 m. Среди всех значений логарифма действительного, как мы уже отмечали, положительного числа, лишь одно действительно совпадает с главным значением логарифма.
m. Среди всех значений логарифма действительного, как мы уже отмечали, положительного числа, лишь одно действительно совпадает с главным значением логарифма.
Легко проверяется равенство
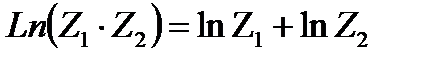
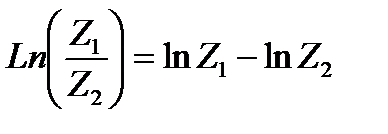
Пример.24.4. Найти число Z, если известно, что LnZ 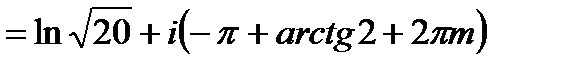 .
.
Решение. Из определения логарифма следует, что 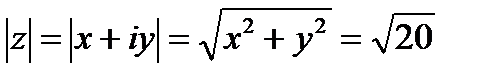 ,
, 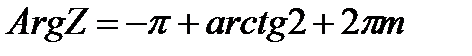 .То есть число Z расположено в третьей четверти, поэтому x<0, y<0. Из условия
.То есть число Z расположено в третьей четверти, поэтому x<0, y<0. Из условия 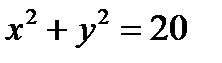 ,
, 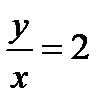 , x<0, y<0, находим x=-2, y=-4. Следовательно, Z=-2-4i.
, x<0, y<0, находим x=-2, y=-4. Следовательно, Z=-2-4i.
Операция 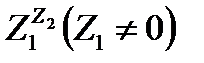 определяется равенством
определяется равенством 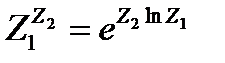 и является также многозначной.
и является также многозначной.
Пример24.5. Число (1+і 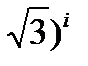 записать в алгебраической форме.
записать в алгебраической форме.
Решение. (1+і 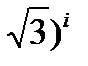 =
= 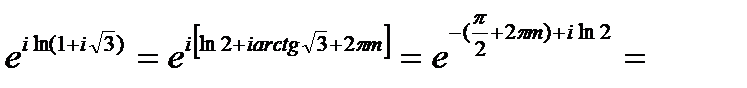
= 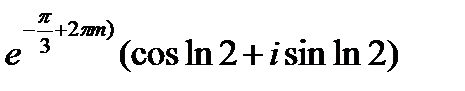
 2015-03-07
2015-03-07 1795
1795








