Элементарные функции

Показательная функция. Функция е^z для комплексных чисел z=x+iy

e^z= e^x+iy=e^x(cosy+isiny)

Следовательно, Im e ^z=e^x siny, ReZ=e^xcosy

Из этого определения вытекает следующие свойства функции e ^z

1. Для любых комплексных чисел z₁ и z₂ имеет место равенство

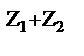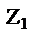е =e e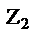

2. Функция e ^z периодична с периодом 2 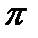i

e ^{z+2 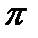i}= e ^z

3. Функция e^z непрерывна во всей комплексной плоскости.

4.Для любого комплексного z=x+iy имеют место равенства e ^z= e ^х (cosy+isiny)

5. Функция e ^z принимает все значения, кроме нуля т.е. уравнение e ^z=А разрешимо для любого комплексного число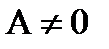

Если =argА то все решения уравнение e^z=А даются формулой

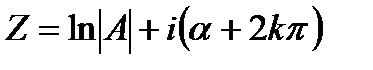, k=0, 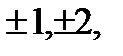(24.8)

В частности, если e^z=1, то

z=2 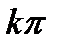i, k= 0, 0,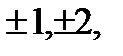

Замечание. Если e^z = A, то комплексное число Z называется логарифмом комплексного числа 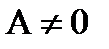и обозначается lnA. Из формулы (24.8) следует, что

lnA = ln|A|+iargA

В частности, ln1=2 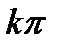i. Ln (-1) = (2k+1) 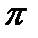i

Lni= (2k+1/2) 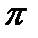i (k- целое число.)