Теорема 25.1. Пусть функция f(z)=u(x,y)+iv(x,y) определена в некоторой окрестности точки Z, причем в этой точке функции U (x,y) и V(x,y) дифференцируемы. Тогда для дифференцируемой функции комплексной переменной f(z) в точке Z необходимо и достаточно, чтобы в этой точке имели место соотношения
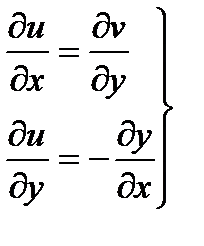 (25.8)
(25.8)
Для производной f(z) справедлива формула
f(z)= 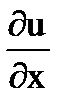 +i
+i 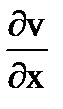 =
= 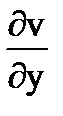 -i
-i 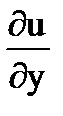 (25.9)
(25.9)
Доказательство. Необходимость. Пусть функция f(z) дифференцируема в точке z. Тогда в силу (25.3) имеем
 f=f¢(z)
f=f¢(z) 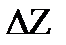 +e(
+e( ) (25.10)
) (25.10)
где 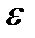 (r)=0(
(r)=0(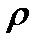 ) при
) при 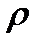
 . Здесь обозначено
. Здесь обозначено
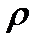 =
= 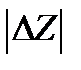 =
= 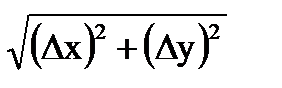
Функцию e(r) комплексной переменной представим в виде  , где функции e1(r), e2(r) принимают действительные значения. Так как e(r)/r
, где функции e1(r), e2(r) принимают действительные значения. Так как e(r)/r  при r
при r  , то e1(r)/r
, то e1(r)/r  , e2(r)/r
, e2(r)/r  при r
при r  , и поэтому
, и поэтому
e1(r)=0(r) e2(r)=0(r) (r  ) (25.11)
) (25.11)
Обозначим  f=
f=  u+i
u+i  v, f(z)=A+iB u подставим в (25.10), тогда получим
v, f(z)=A+iB u подставим в (25.10), тогда получим
 U+i
U+i  V=(A+iB)(
V=(A+iB)( x+i
x+i  y)+e1+ie2 (25.12)
y)+e1+ie2 (25.12)
Приравнивая в этом соотношении действительные и мнимые части, получим
 U=A
U=A  x -B
x -B  y+e1,
y+e1,  V=B
V=B  x +A
x +A  y+e2 (25.13) Тем самым доказано, что функции U,V дифференцируемы в точке (x,y).
y+e2 (25.13) Тем самым доказано, что функции U,V дифференцируемы в точке (x,y).
Из равенств (25.13) находим
A= 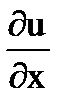 , -B=
, -B= 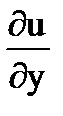 , B=
, B= 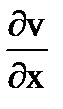 , -A=
, -A= 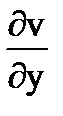 ,
,
откуда следуют условия Коши-Римана и формула (25.8), так как
F(z)=A+iB
Достаточность. Пусть функции U(x,y), V(x,y) дифференцируемы в точке (x,y), и выполняются условия (25.8).
Тогда имеют место равенства (25.13), где e1=0(r), e2=0(r).Умножая второе из этих равенств на і и складывая с первым, получаем
 U +i
U +i  V=A
V=A  х -B
х -B  у +i(В
у +i(В  X+A
X+A  y)+e1+ie2
y)+e1+ie2
или  f=(A+iB)(
f=(A+iB)( x+i
x+i  y)+e1+ie2
y)+e1+ie2
или  f=(A+iB)
f=(A+iB)  z+e(r),
z+e(r),
где e(r)=0(r), откуда в силу (25.3) вытекает дифференцируемость функции f(z) в точке z. Теорема доказана.
 2015-03-07
2015-03-07 1446
1446








