2015-03-07
282
Пусть дана функция f (z)=u(x,y)+iv(x,y). Переменные легко выразить через z=x+iy,
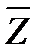=x-iy; x= 
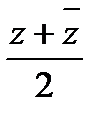, y=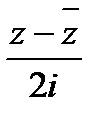 
Поэтому
f(x)= u(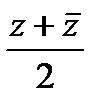
; 
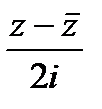)+ iV (
; 
).
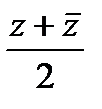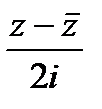То есть функцию f(z) формально можно рассматривать как функцию двух переменных Z и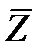 
. Найдем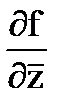 
= 
+ 
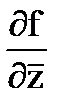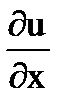
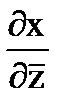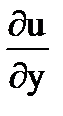
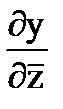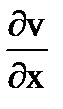
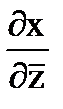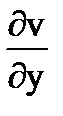
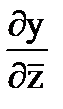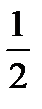
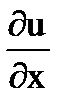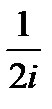
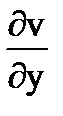+ i (
+ 
)= 
- 
+i(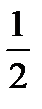 
- )= (
- ) + 
(
+ 
)
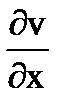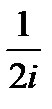
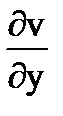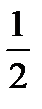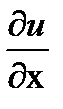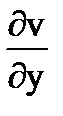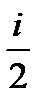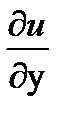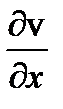В силу (25.8) имеем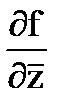 
=0
Теорема 3.4. Условие Коши-Римана и 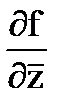=0 эквивалентны.
