1. Дайте определение производной
2. Сформулируйте условие Коши-Римана.
3. Как определяется аналитичность функций?
4. Свойства дифференцируемых функций?
5. Сформулируйте условие Коши-Римана в полярной системе координат.
6. Докажите эквивалентность условий Коши-Римана и 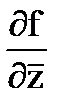 =0.
=0.
7. Какие функции называются регулярными?
Задача 25.1. Восстановить аналитическую в окрестности точки z0 функцию f (z) по известной действительной части (х, у) или мнимой u(x, y) и значению f (z0)
25.1.1 u=x2-y2+x, f (0) =0.
25.1.2 u=x3-3xy+1 f (0) =1.
25.1.3 u=ex(y cos y+x sin y), f (0)=0.
25.1.4 u=x2-y2-2y, f (0)=0.
25.1.5 u= 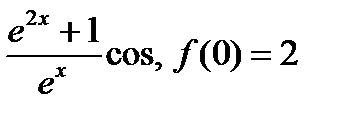
25.1.6 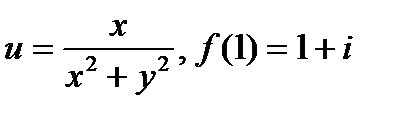 .
.
25.1.7 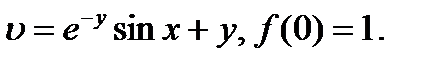
25.1.8 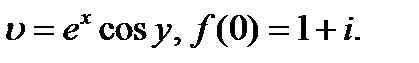
25.1.9 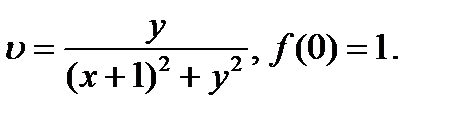
25.1.10 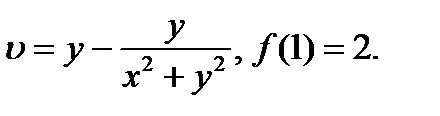
25.1.11 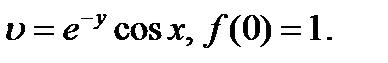
25.1.12 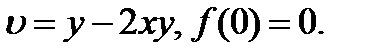
25.1.13 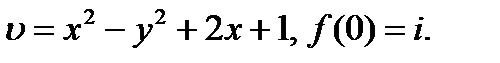
25.1.14 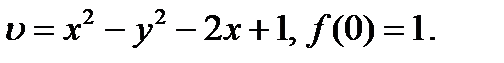
25.1.15 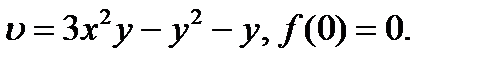
25.1.16 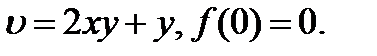
25.1.17 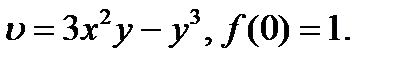
25.1.18 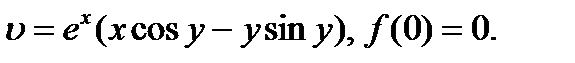
25.1.19 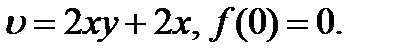
25.20 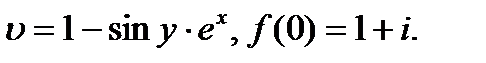
25.21 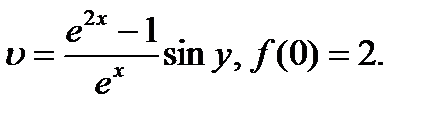
 2015-03-07
2015-03-07 410
410








